AN043 - 采用可变关断时间控制器HFC0300的反激变换器

应用说明

每月为您发送最具参考价值的行业文章

我们会保障您的隐私

摘要

本应用说明介绍了采用MPS 可变关断时间控制器HFC0300实现反激变换器的设计指南，如图 1 所示。遵循本文的步骤，即可轻松设计具有可变关断时间（或准固定导通时间）控制的反激变换器。此外，文章最后一部分还展示了基于设计实例得出的实验结果。

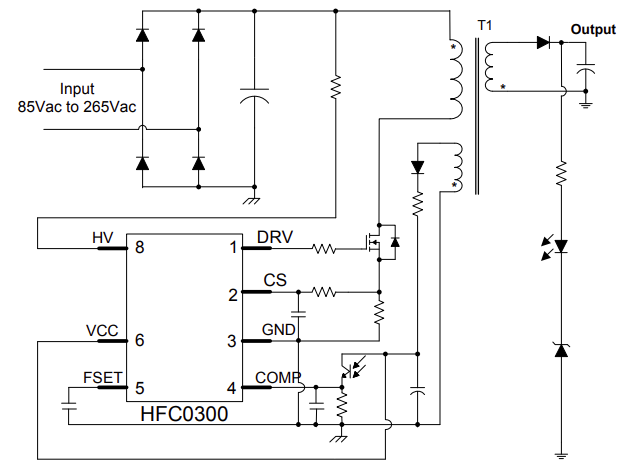
图1: 采用可变关断时间控制器HFC0300实现的反激变换器

HFC0300简介

HFC0300是一款集成了高压电流源的可变关断时间控制器。它采用固定峰值电流技术，随着负载的减轻可降低频率，因此具有出色的轻载效率，同时也可优化其他负载条件下的效率。当输出功率低于给定水平时，控制器将进入突发模式，以进一步减少空载或轻载条件下的功耗。其内部 Vcc 欠压锁定 (UVLO)保护、过载保护 (OLP)、过压保护 (OVP)、短路保护 (SCP) 和过温关断 (TSD)保护功能均集成在 IC 中，以减少外部元件数量。本应用说明介绍了采用 HFC0300 实现离线式反激变换器的实用设计指南，并给出详细的分步设计流程，其中主要包括变压器设计、输出滤波器设计和元件选择。

可变关断时间控制简介

可变关断时间控制是反激变换器的变频控制方案之一。通过实施固定峰值电流模式控制，开关峰值电流被固定（准固定开关导通时间），而关断持续时间则根据所需的输出功率进行调节。在 MOSFET 导通期间，漏极电流增大；一旦漏极电流达到内部固定峰值电流水平，MOSFET 就会关断。反馈环路将根据输出条件控制频率或关断时间。因此，随着负载的减小，关断时间会延长，开关频率也随之降低。随着轻载时频率的降低，所有与频率相关的损耗也相应降低（如栅极驱动损耗、开关损耗、磁芯损耗），从而提高效率。

降低开关频率会迫使变换器工作于可闻区域。为了防止变压器产生机械谐振，HFC0300能够随着负载的减轻逐步降低峰值电流。

图 2显示了关断时间控制反激变换器中原边开关的漏源电压波形。在 MOSFET 导通期间，漏极电流线性增大，直至达到峰值电流水平。然后 MOSFET 关断，反激变压器中的漏感与寄生电容一起振铃，并导致高压尖峰。该尖峰可通过钳位电路来限制。当FSET引脚电压达到COMP（反馈引脚）电平时，开关再次导通并开始新的开关周期。

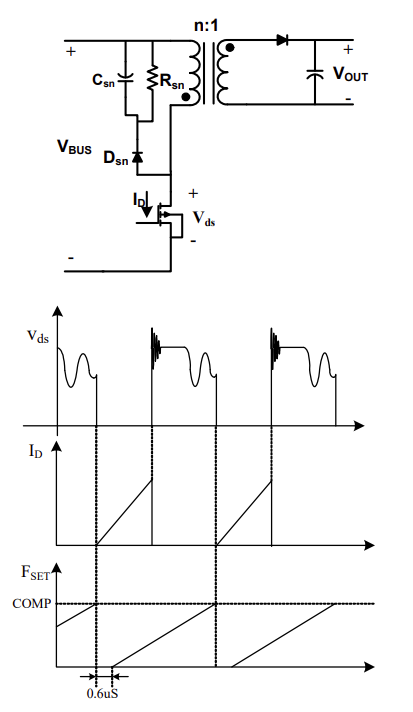
图2: 关断时间反激变换器的关键波形

设计流程

A. 预先确定输入和输出规格

输入交流电压范围：V_ac(min)、V_ac(max)，例如 90V_ac ~ 265V_ac RMS
直流总线电压范围：V_in(max)、V_in(min)
输出：V_o、I_o(min)、I_o(max)、P_out
估计效率：η，用于估计功率转换效率，以计算最大输入功率。一般情况下，根据不同的输出应用，η可设置为0.8~0.9。

最大输入功率的计算公式如下：

$$P_{in} = \frac {P_{out}}{η}$$

图 3 展示了典型的直流总线电压波形。在通用输入条件下，直流输入电容 C_in 通常设置为 2μF/W。对230V单量程应用而言，电容值可减半。

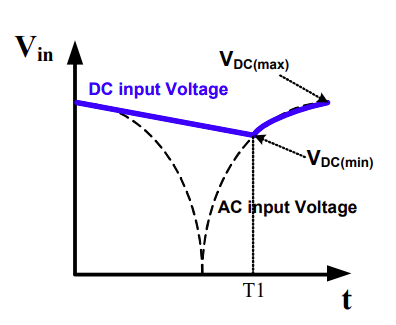
图3: 输出电压波形

根据上述波形可得到交流输入电压 V_AC 和直流输入电压 V_DC：

$$V_{DC}(V_{ac},t)=\sqrt{2 \times V_{ac}^2-\frac{2 \times P_{in}}{C_{in}}\times t}$$

设定 V_AC=V_DC，则直流总线电压达到其最小值 V_DC(min) 时的T1可通过下式计算：

$$V_{DC(min)}=V_{DC}(V_{ac(min)},T1)$$

然后，可得到最小平均直流输入电压 V_in(min)：

$$V_{in(min)}=\frac{\sqrt{2}\times V_{AC(min)}+V_{DC(min)}}{2}$$

以及最大平均直流输入电压 V_in(max)：

$$V_{in(max)}=\sqrt{2} \times V_{ac(max)}$$

B. 确定启动电路

图3所示为启动电路。上电后，内部 2mA 电流源通过连接至 HFC0300 HV 引脚的 R1 对 C1 进行充电。一旦VCC电压达到11.7V，内部高压电流源（2mA）即关闭，IC开始开关，辅助绕组则接管电源。如果在辅助绕组接管电源之前，VCC 已降至 8.2V 以下，则开关停止，内部高压电流源再次开启，它将对 VCC 外部电容 C1 重新充电，从而开始另一个启动过程（见图 4）。

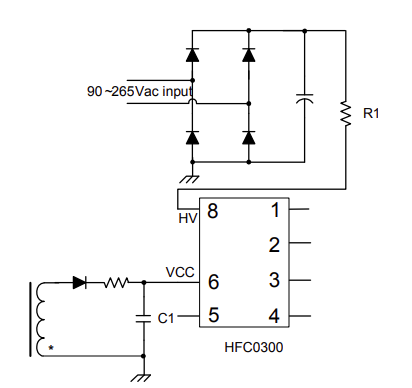
图 4：HFC0300 启动电路

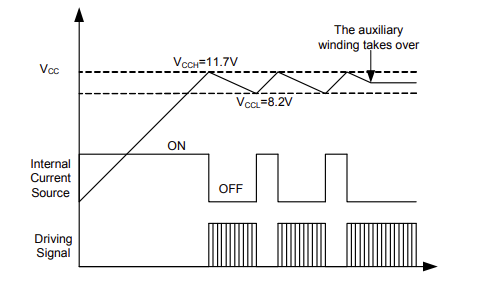
图 5：HFC0300 启动波形和 VCC UVLO

C. 匝数比N、原边MOSFET 和副边整流二极管选择

图 5 显示了反激变换器中原边 MOSFET 和副边整流二极管的典型电压波形。由波形可知，原边MOSFET漏源电压的额定值 V_ds 可通过公式(6)来计算：

$$V_{ds}=\frac {Vin(max)+N\times(V_{out}+V_F)+60V}{k}$$

其中，k是降额因子，通常选择为0.9；V_F是整流二极管的正向电压；此处假设尖峰电压为60V。

副边整流二极管额定电压 V_ka 可通过公式 (7) 来估算：

$$V_{ka}=\frac {\frac{Vin(max)}{N}+V_{out}}{k}$$

其中k是降额因子，通常选择为0.9。

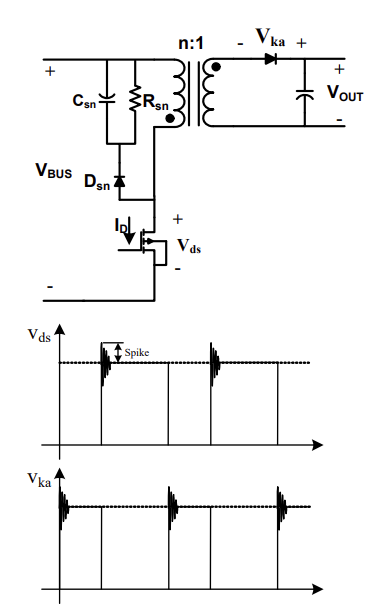
图 6：原边MOSFET 和副边整流二极管的电压应力

根据公式 (6) 和 (7)，可以计算出原边 MOSFET 和副边整流二极管的额定电压与匝数比 N 的关系，如图 6 所示。

例如在一个90Vac~265Vac输入、19V输出适配器应用中，推荐选择650V MOSFET和100V整流二极管以获得更好的性能。从图 7可以看出，N=6可满足额定电压要求。

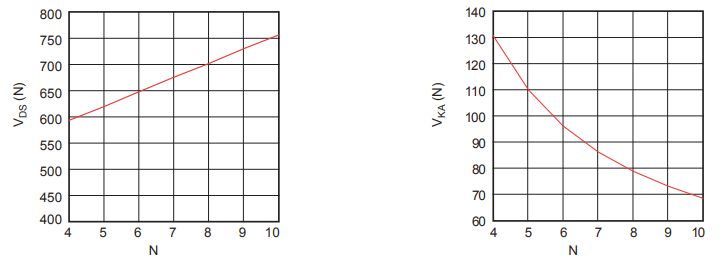
图 7：原边 MOSFET 和副边整流二极管的电压应力额定值

D. 电流采样电阻

峰值电流水平内部设置为0.5V，因此电流采样电阻可用于设置原边峰值电流，同时决定变换器的工作模式，如CCM、BCM或DCM。如果电源被设计为在低线电压输入时以 BCM 模式运行，那么在高线电压输入和相同负载条件下将以 DCM 模式运行。磁化电感电流（反映至原边）和原边 MOSFET 的漏源电压如图 8 所示。

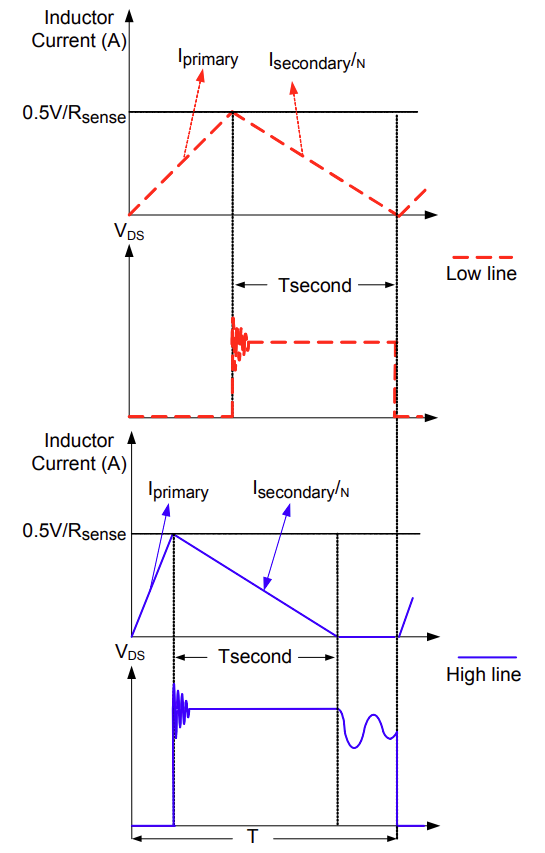
图 8：不同线电压下的原边 MOSFET 电感电流和电压

副边电流的持续时间可通过公式（8）计算：

$$T_{second}=\frac {L_m \times I_{peak}}{N \times V_O}$$

其中，L_m为原边磁化电感，I_peak 为原边峰值电流。由于在不同输入和相同输出条件下的 I_peak 总是相同，因此副边电流的持续时间也是相同的。开关周期可以通过公式(9)计算：

$$T=\frac{N \times I_{peak} \times T_{second}}{2 \times I_o}$$

根据公式(9)可知，在不同输入和相同输出条件下，开关周期也始终保持一致。由于原边开关导通时间随着输入电压的增加而减小，因此，输入线电压越高，其进入的DCM模式就越深。通常应在最小输入条件下设计参数，以确保变换器能够在最小输入条件下提供所需的输出功率。

由于N已选定，因此，如果电源设计为在低线电压下以边界电流模式 (BCM) 运行，则峰值电流可通过公式 (10)轻松计算：

$$I_{peak\_BCM}=\frac{2I_o}{1-D}$$

其中D为开关占空比，可通过公式(11)计算：

$$D=\frac {(V_o+V_F)\times N}{V_{in}+(V_o+V_F)\times N}$$

如果电流采样电阻设定的峰值电流大于 I_{peak_BCM}，则电源进入DCM模式；反之，如果电流采样电阻设置的峰值电流小于 I_{peak_BCM}，则电源将进入CCM模式，如图9所示。这里的 K_depth 被定义为CCM的深度。

$$K_{depth}=\frac{I_{valley}}{I_{peak}}$$

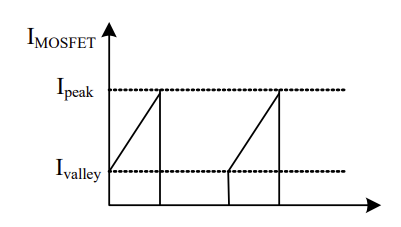
图9: CCM模式下的原边电流

峰值电流可由公式（13）计算得出：

$$I_{peak}=\frac {2I_o}{(1-D)\times(1+K_{depth})\times N}$$

通常，40W 以下的功率级别优选 BCM（边界电流模式）；功率水平高于40W时选择CCM（连续电流模式）。提供的功率越高，应采用更深的 CCM，从而实现更高的效率与满载散热性能。例如，对于90W的电源，K_depth可选择0.5。

所以，当给定电源规格后，我们首先需要确定变换器的工作模式，即确定 K_depth。I_peak 和 I_valley 可以通过公式(10)至(13)计算。电流采样电阻则根据公式（14）来选择：

$$R_{sense}=\frac{V_{peak}}{I_{peak}}$$

其中 V_peak 是电流采样电阻的峰值电压阈值；对HFC0300来说是恒定的0.5V。然后，我们根据公式（15）中给出的功耗来选择具有适当额定功率的电流电阻：

$$P_{sense}=[(\frac{I_{peak}+I_{valley}}{2})^2+\frac{1}{12}(I_{peak}-I_{valley})^2]\times D \times R_{sense}$$

E. 原边电感Lm

反激变换器能够提供的功率与存储在其原边电感 Lm 中的能量相关，如CCM模式下的公式 (16) 和DCM模式下的公式 (17)。

$$\frac {1}{2} \times L_m \times (I_{peak}^2 - I_{valley}^2) \times f_s = \frac {p_{o\_CCM}}{η}$$ $$\frac {1}{2} \times L_m \times I_{peak}^2 \times f_s = \frac {p_{o\_CCM}}{η}$$

调节输出功率的方法有两种，调整峰值电流值（传统峰值电流模式控制）和/或调整开关频率。HFC0300 通过调整开关频率来调节输出功率，同时保持峰值电流值恒定。因此，一旦选定了峰值电流，反馈环路就会自动设置开关频率以获得所需的输出功率。

由于 I_peak 和 I_valley 在设计之初已经确定，因此如果选定了 fs，就可以计算出 Lm。要提供良好的 EMI 性能，65kHz的最高频率通常是一个不错的选择，因为其二次谐波（2*65kHz）的传导 EMI 噪声仍未经过测试（传导 EMI 频率范围：150kHz~30MHz）

如 D 部分所述，在理想情况下，不同输入线电压和相同输出功率条件下的开关频率是相同的。但在实际电路中，情况略有不同。尽管阈值是恒定的，但由于不可避免的传播延迟，高线电压的峰值电流将比低线电压的峰值电流稍高一些，开关频率将在低线电压和满载条件下达到最大值。所以我们通常选择65kHz为低线满载时的频率。而所有计算都是在最低线电压情况下进行。

F. C_FSET 和OLP功能的设计

如图 10 所示，最大频率根据连接到 FSET 引脚的电容 C_FSET 的充电结束时间来设定。在原边开关导通后的很短时间之后（约 0.6us），恒流源开始为电容充电，并将其电压与来自反馈环路的 COMP 电压进行比较（见图 10）。一旦该电容电压达到阈值，电容即快速放电至 0V，并开始新的周期。为了使 FSET 引脚上的电压完全放电，在 C_FSET 再次充电之前，有大约 0.6μs 的内部延迟（见图 11）。因此，开关频率可由 VCO（压控振荡）等反馈环路进行调节。连接到 FSET 引脚的电容可通过公式（18）计算：

$$C_{FSET} = \frac {28uA \times (\frac {1}{f_{max}}+0.6us)}{0.88V}$$

其中，f_max为最大频率，由连接到 FSET 引脚的电容设置。

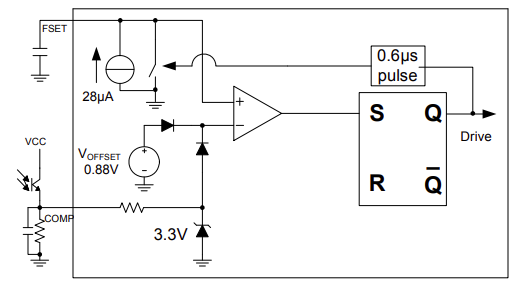
图 10：VCO（压控振荡）工作模式

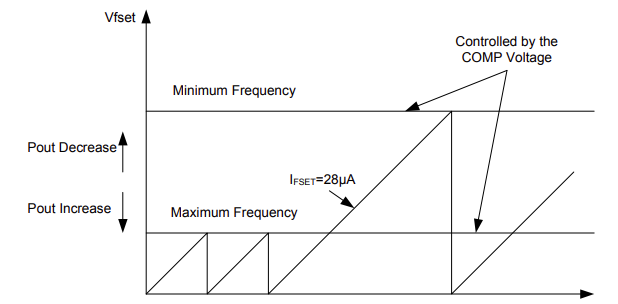
图 11：COMP 电压调整开关频率

如上所述，开关频率在低线电压和满载时达到最大值。我们将该频率定义为fs（此处选择65kHz），最大频率(f_max)设置为约 110%的fs。频率随着输出功率的增加而提高。当频率达到C_FSET设置的最大频率时，会发生过功率限制，导致输出电压无法维持，从而使COMP 饱和并低于 OLP（过载保护）阈值（0.85V）。

HFC0300 采用独特的数字定时器方法来实现过载保护 (OLP)。当COMP低于0.85V错误标志时，定时器开始计数。如果错误标志被移除，则定时器重置。如果计数达到 6000 ，则定时器溢出，触发 OLP。定时器的持续时间可避免在电源处于启动或负载过渡阶段时触发 OLP 功能。因此，启动期间，应在 6000 个开关周期以内建立输出电压。