Introduction and Principle of Operation

Boost converters are a type of DC-DC switching converter that efficiently increase (step-up) the input voltage to a higher output voltage. By storing energy in an inductor during the switch-on phase and releasing it to the load during the switch-off phase, this voltage conversion is made possible. Power electronics applications requiring a greater output voltage than the input source, in particular, depend on boost converters.

The basic principle of operation for a boost converter can be understood through the following two stages:

Switch-on period (S1 closed, S2 open): During this stage, the input voltage (Vin) is applied across the inductor (L), causing the current through the inductor to increase linearly. The energy stored in the inductor builds up, and the diode (D) is reverse-biased, preventing current flow to the load. The inductor current can be expressed as:

$$\Delta I_L = \frac{V_{in}}{L} \cdot t_{on}$$

where ΔIL is the change in inductor current, L is the inductance, and t_on is the duration of the switch-on period.

Switch-off period (S1 open, S2 closed): When the switch S1 opens, the inductor current must continue to flow. This forces the diode D to become forward-biased, and the inductor releases its stored energy to the load (R) and the output capacitor (C). During this period, the voltage across the inductor (VL) is equal to the difference between the output voltage (Vout) and the input voltage (Vin). The inductor current decreases linearly as the energy is transferred to the load, and the equation for the inductor current becomes:

$$\Delta I_L = \frac{(V_{out} - V_{in})}{L} \cdot t_{off}$$

where t_off is the duration of the switch-off period.

By equating the inductor current equations for both stages and rearranging the terms, we can derive the voltage conversion relationship for the boost converter:

$$V_{out} = \frac{V_{in}}{(1 - D)}$$

where D is the duty cycle, defined as the ratio of the switch-on time (t_on) to the total switching period (T), or

$$D=\frac {t_{on}}{(t_{on}+T_{off})}$$

This equation shows that the output voltage can be controlled by adjusting the duty cycle of the switching waveform, allowing for a higher output voltage than the input voltage. In the next sections, we will further explore the circuit topology, key components, conduction modes, design considerations, efficiency, and applications of boost converters, providing a comprehensive understanding of their operation and uses in power electronics systems.

Circuit Topology and Key Components

In this converter topology, the magnetic energy of the inductor is used to transfer energy from a lower voltage DC source to a higher load voltage. By turning on the switch S, the inductor is connected to the DC power supply E (Figure 5). The diode D is reverse-biased by the voltage at the load that is supplied with energy from the capacitor. Under the influence of voltage E, the inductor current linearly increases from its minimum to maximum value (Figure 7).

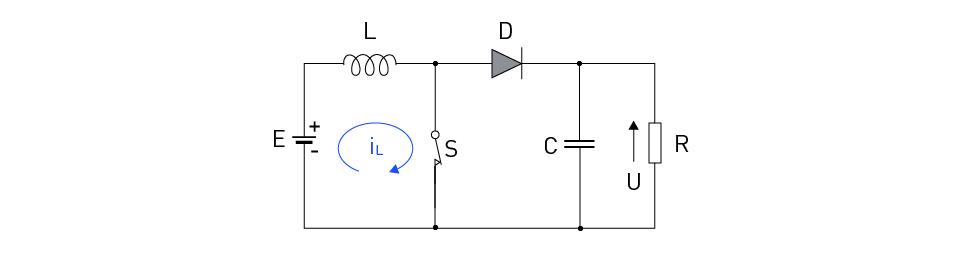
Figure 5: The Boost Converter Circuit Diagram – Interval t_ON

After the t_ON interval elapses, the switch S is turned off. In the subsequent time interval (t_OFF), the inductor current, which is a result of the accumulated magnetic energy, flows through the diode to the load, transferring energy from the DC source and inductor to the load (Figure 6).

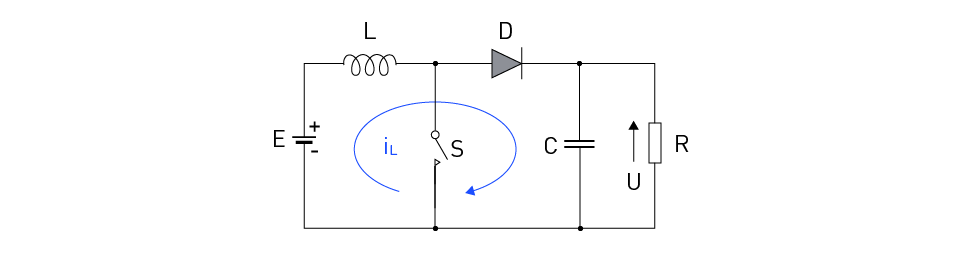
Figure 6: The Boost Converter Circuit Diagram – Interval t_OFF

In this period, the voltage across the inductor changes direction and becomes equal to the difference between the voltage on the load and the DC supply voltage. Under the influence of this voltage, the inductor current decreases from its maximum to its minimum value (Figure 7). In the steady state, the average voltage value on the inductor is equal to zero:

$$E \cdot t_{ON} = (U - E) \cdot t_{OFF}$$ $$\Rightarrow U = E \frac{1}{\frac{t_{OFF}}{t_{ON}+t_{OFF}}} = E \frac{1}{\frac{T-t_{ON}}{T}} = E \frac{1}{1-\frac{t_{ON}}{T}} = E \frac{1}{1-d}$$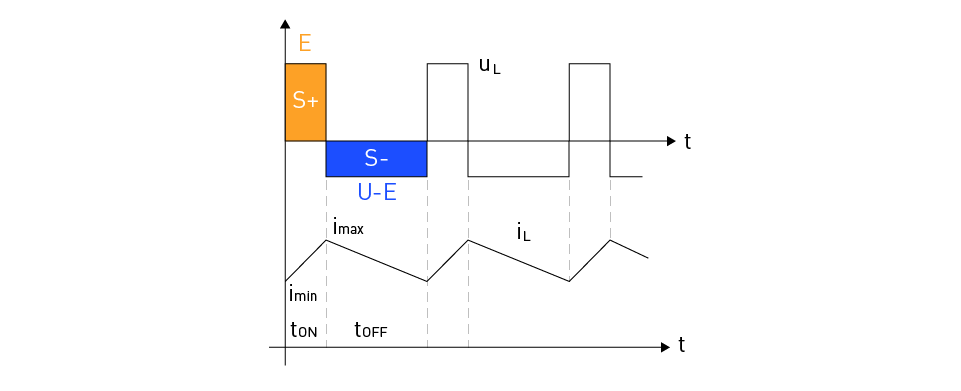

Figure 7: The Boost Converter - Inductor Voltage and Current Versus Time Graph

From the previous equation, it can be seen that the voltage at the load will be equal to the voltage of the DC source if d = 0, and will increase with an increase in the active part of the period (t_ON), confirming that this is a voltage-boosting chopper. The same equation also shows that the voltage at the load will be infinitely large if d = 1, which is not possible because the duty cycle equal to 1 implies that t_ON = T or t_OFF = 0, which further implies that the switch S is never turned off and thus no energy transfer will occur from the DC source to the load, resulting in the load voltage being equal to zero.

A boost converter is a popular and widely used DC-DC converter topology that steps up the input voltage to a higher output voltage. The basic circuit topology of a boost converter consists of the following key components:

Inductor (L): The inductor, which stores and releases energy throughout the switching cycles, is an essential part of the boost converter. Its major job is to preserve energy storage during conversion while controlling current flow.

Switch (S): The switch, By alternating disconnecting and connecting the inductor to the load, the switch (usually a MOSFET or IGBT) plays a crucial role in managing the energy transfer between the input and output.

Diode (D): During the switch-off time, the diode only permits current to flow in one direction in the circuit—toward the output. When the switch is open, it stops the current from returning to the input side.

Output capacitor (C): The output capacitor is in charge of stabilizing the voltage across the load and smoothing the output voltage. It guarantees a constant output voltage for the load and filters out high-frequency voltage ripples.

Load resistor (R): The load resistor (R) symbolizes the electrical load that is linked and powered by the boost converter. The converter has to be built to give this load the necessary voltage and current.

The basic operation of the boost converter can be summarized as follows: During the switch-on period, the inductor stores energy from the input voltage source while the diode prevents current flow to the load. When the switch is turned off, the inductor releases its stored energy through the diode, giving the load a higher voltage than the input voltage. The output capacitor smooths the output voltage, delivering a stable supply to the load.

Continuous and Discontinuous Conduction Modes

In the analysis and design of boost converters, it is crucial to consider the two primary conduction modes: continuous conduction mode (CCM) and discontinuous conduction mode (DCM). Both modes differ in the behavior of inductor current, which affects the converter's performance, efficiency, and design criteria.

Continuous Conduction Mode (CCM): In CCM, the inductor current remains positive and never reaches zero throughout the switching cycle. The inductor current grows during the switch-on phase, storing energy in its magnetic field. The inductor current drops as it transfers its stored energy to the output when the switch is switched off. The current waveform in CCM has a triangle shape, and the load current is equal to the average value of the current.

Lower peak currents and output voltage ripple are produced by CCM operation, boosting efficiency and reducing strain on the converter's parts. To sustain continuous current flow, greater inductor values are also necessary, which could result in an increase in the converter's size and price.

Discontinuous Conduction Mode (DCM): In DCM, during a portion of the switching cycle, the inductor current drops to zero, signifying that the energy transfer to the output is finished before the start of the subsequent switch-on period. There is a zero-current interval between the switch-off and the subsequent switch-on periods, giving the inductor current waveform in DCM a trapezoidal shape.

Smaller inductor values are possible with DCM operation, which results in compact and affordable converter designs. In contrast to CCM, it also leads to larger peak currents, increased output voltage ripple, and lower efficiency. DCM is more frequently used in applications with a wide range of load circumstances or light loads.

Design Considerations and Calculations

Component selection, input/output voltage and current requirements, switching frequency, and target efficiency are just a few of the variables that must be carefully considered when designing boost converters. The main design factors and calculations for creating a boost converter are covered in this section.

Input and Output Specifications: Before choosing the converter components, it is necessary to determine the application’s requirements for the input and output voltage (Vin and Vout) and current (Iin and Iout). The converter’s needed voltage conversion ratio, duty cycle, and power handling capacity will all be determined by these criteria.

Duty Cycle: The duty cycle (D) is the ratio of the switch-on time to the total switching period. In a boost converter, the duty cycle determines the relationship between the input and output voltages as follows:

$$D = \frac{(V_{out} - V_{in})}{V_{out}}$$

This equation is valid for the continuous conduction mode (CCM) operation. The duty cycle is important for selecting the appropriate switching frequency and inductor value.

Switching Frequency: The converter's efficiency, transient response, and size of the passive components are all impacted by the switching frequency (fs). Compact designs are made possible by the lower inductor and capacitor values at higher switching frequencies. The larger switching losses and decreased efficiency could result from the higher switching frequency. Size and efficiency must be compromised while choosing the switching frequency.

Inductor Selection: The inductor value (L) is crucial for maintaining the desired conduction mode (CCM or DCM) and ensuring stable operation. The inductor value can be calculated using the following equation for CCM operation:

$$L = \frac{(V_{in} \cdot D)}{(f_s \cdot \Delta I_L)}$$

1) First approach:

$$\Delta I_L = \frac{V_{in}}{L} \cdot t_{ON} = \frac{V_{in}}{L} \cdot d \cdot T = \frac{(V_{in} \cdot d)}{(L \cdot f_s)} \Rightarrow L = \frac{(V_{in} \cdot d)}{(f_s \cdot \Delta I_L)}$$

2) Second approach:

$$\Delta I_L = \frac{(V_{out} - V_{in})}{L} \cdot t_{OFF} = \frac{ \frac{V_{in}}{(1-d)} - V_{in}}{L} \cdot (T - t_{ON}) = \frac{(V_{in} \cdot d)}{(1-d) \cdot L} \cdot T \cdot (1 - d) \Rightarrow L = \frac{(V_{in} \cdot d)}{(f_s \cdot \Delta I_L)}$$

where ΔIL is the peak-to-peak inductor current ripple. A smaller inductor value will result in a higher current ripple, which may affect the output voltage ripple and converter efficiency.

Capacitor Selection: The output capacitor (Cout) helps to filter the output voltage ripple and ensure a stable output. The output capacitor value can be determined using the following equation:

$$C_{out} = \frac{(I_{out} \cdot D)}{(f_s \cdot \Delta V_{out})}$$

The output capacitor (Cout) controls converter stability by filtering output voltage sag. We must take into account the intended output voltage ripple (Vout), the load current (Iout), the duty cycle (D), and the switching frequency (fs) to obtain the proper value for Cout. The output voltage ripple (ΔVout) is mainly due to the inductor current ripple (ΔIL) charging and discharging the output capacitor during the switching cycle. In a boost converter, the inductor current ripple (ΔIL) flows through the output capacitor during the off-time of the switch (t_OFF), when the diode is conducting.

Let us first consider the capacitor current (Ic) during the off-time (t_OFF). As the inductor current (IL) is approximately constant during this period, we can approximate the capacitor current as follows:

$$I_c \approx \Delta I_L \cdot (1 - D)$$

Now, let us consider the relationship between the current and capacitance in the time domain:

$$I_c = C \cdot \frac{dV}{dt}$$

Where 'Ic' is the capacitor current, 'C' is the capacitance value, 'dV' is the change in voltage across the capacitor, and 'dt' is the change in time.

Combining these two relationships, we get:

$$\Delta I_L \cdot (1 - D) \approx C_{out} \cdot \frac{\Delta V_{out}}{T}$$

Where 'T' is the switching period (1/fs), and 'ΔVout' is the desired output voltage ripple.

Now, we can rearrange the equation to solve for Cout:

$$C_{out} \approx \frac{\Delta I_L \cdot (1 - D) \cdot T}{\Delta V_{out}}$$

However, it is important to note that the inductor current ripple (ΔIL) is directly proportional to the output current (Iout) and the duty cycle (D). A higher output current will lead to a larger inductor current ripple. Thus, we can rewrite the equation for Cout by substituting the proportionality relationship between ΔIL and Iout * D:

$$C_{out} \approx \frac{I_{out} \cdot D \cdot T}{\Delta V_{out}}$$

where ΔVout is the desired peak-to-peak output voltage ripple. A larger capacitor value will reduce the output voltage ripple but may increase the size and cost of the converter.

Switch and Diode Selection: The voltage, current, conduction, and switching losses of the switch (often a MOSFET) and the diode must be taken into consideration while choosing them. While the current rating should surpass the peak current in the converter, the voltage rating should be greater than the maximum voltage across the switch and diode when it is operating.

Efficiency and Losses

In a boost converter, efficiency is a crucial parameter determining how effectively it transfers power from input to output. The efficiency (η) of a boost converter can be expressed as the ratio of output power (Pout) to input power (Pin):

$$\eta = \frac{P_{out}}{P_{in}}$$

The losses in a boost converter can be attributed to several factors, which will be discussed in this section.

Conduction Losses: The resistance of circuit elements like the inductor, switch (MOSFET), and diode causes conduction losses. These losses are directly related to the resistance of the components and the current that flows through them. By choosing parts with lower resistances and improving the converter's design for low current flow, conduction losses can be reduced.

Switching Losses: When a MOSFET switches between its on and off states, switching losses occur. During these transitions, the switch is experiencing both voltage and current, which results in power loss. The MOSFET's on-state resistance, drain-to-source voltage, and switching frequency all influence the overall switching loss. A MOSFET with low on-state resistance and quick switching periods should be used to reduce switching losses.

Diode Reverse Recovery Losses: A diode experiences reverse recovery as it transitions from the conducting state to the blocking state. Power loss occurs as a result of the diode briefly conducting current in the opposite direction during this process. A Schottky diode or other diode with a short reverse recovery time should be chosen to reduce these losses.

Magnetic Core Losses: The alternating magnetic field inside the inductor core results in energy dissipation in the form of heat and causes inductor core losses. The core material, operation frequency, and magnetic flux density all affect these losses. To reduce core losses, an appropriate core material should be selected, and the inductor design should be optimized to minimize the magnetic flux density.

Capacitor Losses: Equivalent series resistance (ESR) of the output capacitor is the principal cause of capacitor losses. These losses lead to the production of heat and a decline in general efficiency. These losses can be reduced by using capacitors with a low ESR.

Applications and Examples

Boost converters are widely used in various applications due to their ability to step up the input voltage. This section will discuss some common applications and examples of boost converters in real-world scenarios.

Power Supplies: Boost converters are utilized in power supplies to produce a stable, higher output voltage from a lower input voltage source, making them useful for portable devices and battery-operated systems where input voltage may vary due to battery discharge or other factors. Examples include laptop chargers, USB power adapters, and portable power banks.

LED Lighting: In LED lighting systems, boost converters are used to maintain a constant current to the LED string, ensuring consistent brightness even when the input voltage fluctuates. This is particularly relevant in automotive applications, where the vehicle's electrical system voltage can vary, and the boost converter ensures stable LED illumination.

Solar Power Systems: Boost converters play a critical role in solar power systems,, particularly in maximum power point tracking (MPPT) controllers. The converter adjusts its output voltage to extract the maximum power from the solar panels, stepping up the panel voltage to charge batteries or supply power to the electrical grid.

Electric Vehicles: Boost converters are used in electric vehicles to increase the voltage from the battery pack to a higher voltage level required for various electrical components such as the traction motor, air conditioning system, or power steering. This enables efficient power delivery and optimal vehicle performance.

Telecommunications: Boost converters are employed in telecommunications applications to produce stable, higher output voltages from lower input voltages, ensuring the reliable operation of radio frequency (RF) transmitters, base stations, and other communication equipment.

Sensor Systems: Boost converters are commonly used in sensor systems to provide a stable voltage supply for analog-to-digital converters (ADCs) and other sensitive electronic components. This is especially important in sensor systems operating in environments with variable input voltage conditions, such as remote monitoring systems powered by batteries or energy harvesting devices.