如何设计超宽输入电压范围反激式变换器

Joan Mampel

每月为您发送最具参考价值的行业文章

我们会保障您的隐私

引言

在现代技术中，反激式变换器是家庭和工业应用中广泛使用的拓扑结构之一，常用于需要辅助电源的场景。这种拓扑如此流行，设计者们常常会尝试创建具有超宽输入电压范围（VIN）的统一单设计方案，以最大限度发挥反激式变换器的功能，同时避免长期验证问题。

本文将介绍如何利用MP023来设计具有超宽输入电压范围的反激式变换器。MP023 是一款适用于低功率应用的原边调节（PSR）控制器，它能够提供精确的恒压和恒流输出。我们将以 MP023 为例，展示一个 15W/5V 反激式变换器的设计，该变换器可接受交流和直流输入电压，并支持在宽输入电压范围内工作。

MP023：原边调节反激式控制器

MP023 是一款离线式原边控制器，它能够提供极佳的集成调节功能，无需光耦合器或副边反馈电路。

MP023 的可变关断时间控制使反激式变换器能够在断续导通模式（DCM）下工作。该器件的电流限制和最大副边占空比均可配置，因此输出电流（I_OUT）的设置也变得很简单。图 1 展示了 MP023 的典型应用电路。

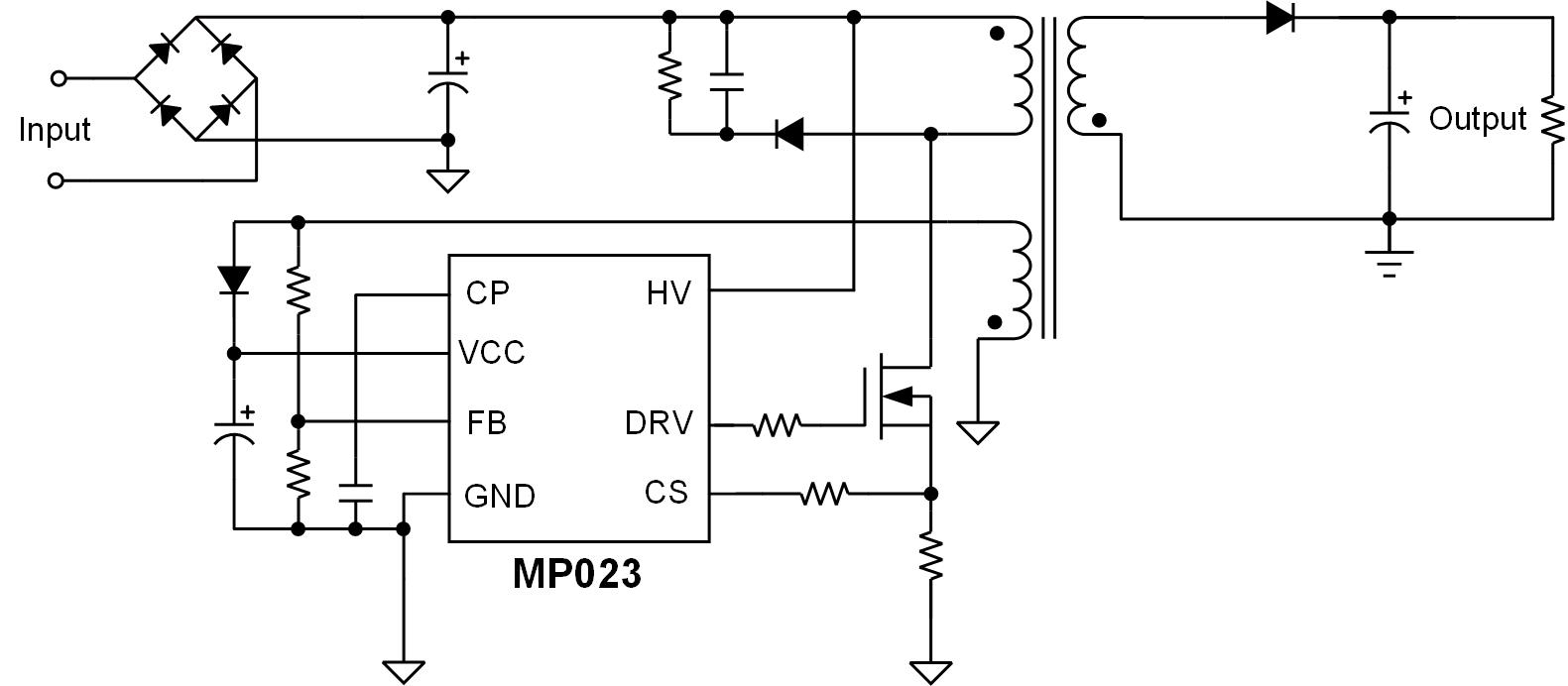
图1: MP023典型应用电路

MP023通过内部高压启动电流源和节能技术将空载功耗限制在 30mW 以下，同时提供全面的保护功能，包括V_CC欠压锁定 (UVLO)保护、过载保护 (OLP)、过温保护 (OTP)、开环保护 (OCkP) 和过压保护 (OVP)。

反激式变换器的设计流程

设计具有超宽V_IN范围的反激式变换器需要考虑并权衡很多重要因素。下文将详细介绍设计流程中的每个步骤。

图 2 所示为反激式变换器的设计流程图。

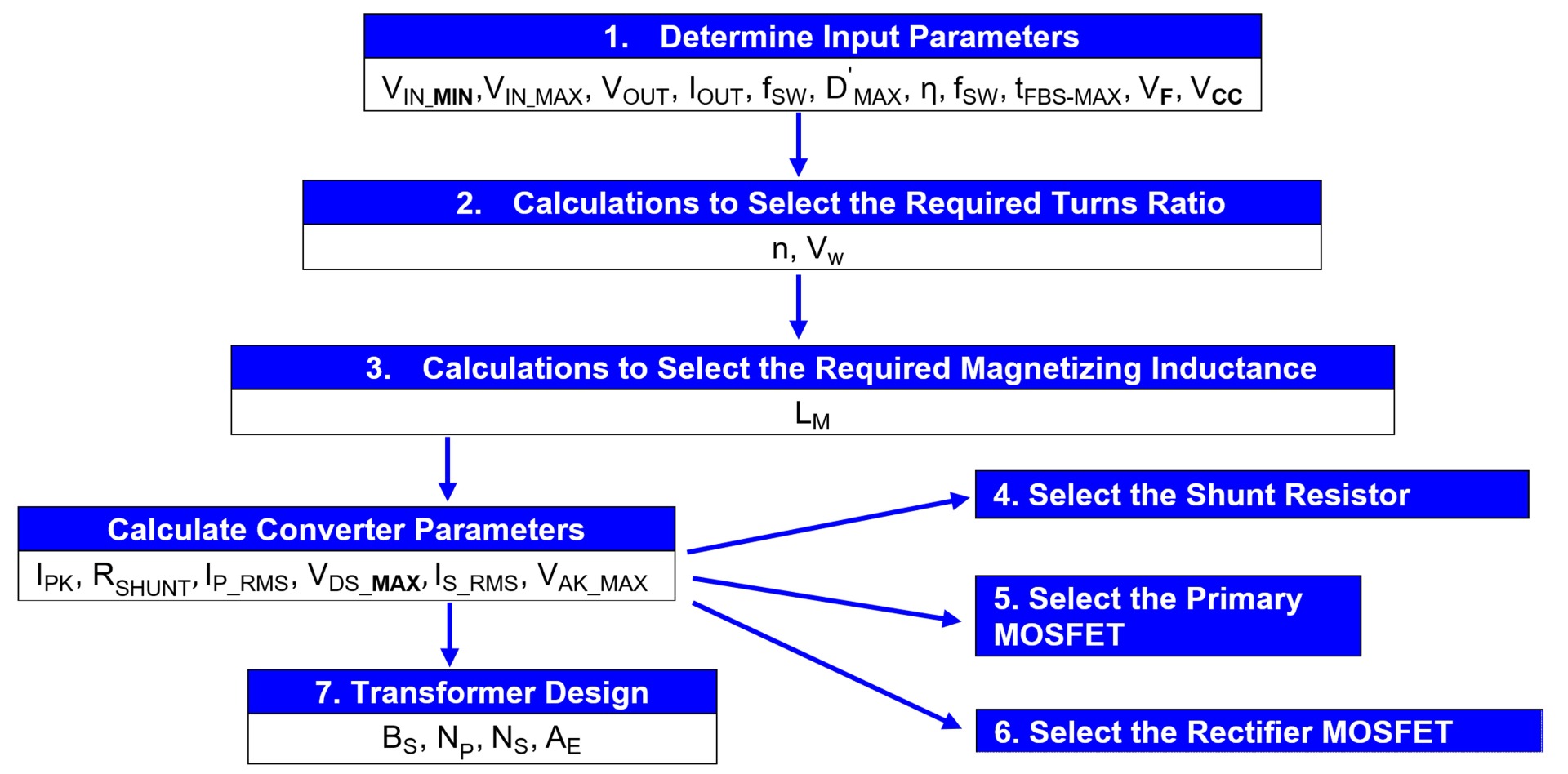
图 2：控制环路设计流程图

反激式变换器的设计流程与相关计算

步骤 1：设计输入

设计变换器需要首先确定输入参数。这些参数包括输入电压（V_IN）、输出电压（V_OUT）、输出电流（I_OUT）、工作模式、开关频率（f_SW）、副边占空比、估计效率、反馈 (FB) 最大采样时间、副边 FET 的正向电压以及 IC 电源电压。

表 1罗列出了本文讨论电路的设计输入。在本例中，输入电压范围为85V_AC至576V_AC，或90V_DC至815V_DC，可以是交流或者直流输入。

表1:设计输入一览

设计输入	值
最小输入电压（V_{IN_MIN}）	85V_AC（或90V_DC）
最大输入电压（V_{IN_MAX}）	576V_AC（或815V_DC）
输出电压（V_OUT）	5V
输出电流（I_OUT）	3A
操作模式	DCM
开关频率（f_SW）	50kHz
副边占空比（D’_MAX）	40%
预估效率（η）	85%
整流管MOSFET正向电压（V_F）	0.1V
IC 电源电压	12V

MP023 具有输出电缆补偿功能，根据连接到 CP 引脚的电阻或电容，副边占空比可限定为特定的值。如MP023 数据手册所述，将 1µF 电容连接到 MP023 的 CP 引脚会将副边占空比限制为 40%。

为了确保结果符合实际应用，变换器的预估效率被定义为相对较低（约 85%），这是低功耗反激式变换器的常见效率值。在本应用中，I_OUT被定义为 3A，且同步整流控制器（例如 MP6908A）与副边 MOSFET 配合工作以提高效率并改善散热。

步骤 2：计算并选择所需匝数比

由于副边最大占空比有所限制，因此需要根据指定的V_{IN_MIN}计算最大匝数比 (n)，以提供足够的I_OUT。最大匝数比可以通过公式 (1) 来计算：

$$\begin{align*} n &< \left(1 - D'_{\text{MAX}}\right) \times V_{\text{DC}} / \left(V_{\text{OUT}} + V_F\right) \times D'_{\text{MAX}} \\ &\rightarrow n < \left(1 - 0.4\right) \times 90 / \left(5 + 0.1\right) \times 0.4 \\ &\rightarrow n < 26.47 \end{align*}$$

计算出最大匝数比，以V_{IN_MIN}提供最大功率，然后选择合适的 n。最大匝数比的选择需要在副边 RMS 电流和副边 MOSFET 最大反向电压之间进行权衡。

本例利用了同步整流，因此副边 MOSFET 的反向电压很重要，因为低压 MOSFET 具有高性价比且更容易获得。本设计选择的最大匝数比为15；我们将在步骤 5 中对其进行验证。

接下来，计算原边绕组在开关周期的后半部分将经历的输出反射电压（V_W）。V_W可以通过公式 (2) 来估算：

$$V_w = n \times (V_{\text{OUT}} + V_F) = 15 \times (5 + 0.1) = 76.5V$$

V_W对计算原边 MOSFET 的最大反向电压很重要。

步骤 3：计算并选择所需磁化电感

由于补偿器的无源元件集成在控制器内部，因此 MP023 可以对其提供的辅助电压进行采样，以实现闭环增益系统（反激式变换器和集成补偿器）。FB 最大采样时间定义了控制器对辅助电压进行采样以进行调节的时间（见图 3）。

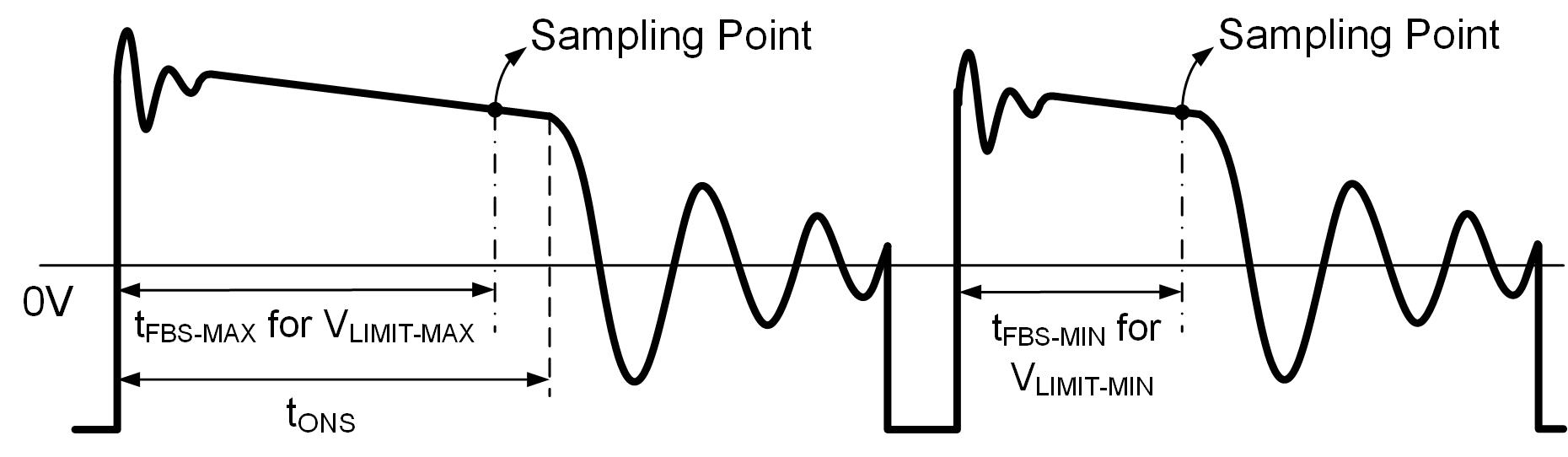
图 3：FB 电压采样点

MP023副边 MOSFET 的最小导通时间（t_{S_ON}）必须满足公式 (3) 中的要求：

$$t_{\text{S_ON}} = I_{\text{PK}} \times \frac{N_{\text{S}} \times L_{\text{M}}}{(V_{\text{OUT}} + V_{\text{F}}) \times N_{\text{P}}} > t_{\text{FBS_MAX}} + t_{\text{FBS_SD}}$$

其中t_{FBS_MAX}为 FB 最大采样时间，t_{FBS_SD}为 FB 采样持续时间。

磁化电感及其峰值电流值的计算则需要考虑工作模式。在本例中，MP023 工作在 DCM 模式下，因此可以使用公式 (4) 来估算输出功率 (P)：

$$P = \eta \times \frac{1}{2} \times L_{M} \times I_{PK}^2 \times f_{SW}$$

根据公式 (3) 和公式 (4) ，最小磁化电感可以通过公式 (5) 来计算：

$$L_{\text{M_MIN}} > \left( \frac {(t_{\text{FBS_MAX}} + t_{\text{FBS_SD}}) \times N_{PS} \times (V_{\text{OUT}} + V_F) \times \sqrt{f_{SW}}} {\sqrt{2 \times P_{OUT}}} \right)^2$$

带入值进行计算：

$$L_{\text{M_MIN}} > \left( \frac{(3.5 \times 10^{-6} + 330 \times 10^{-9}) \times 15 \times (5 + 0.1 ) \times \sqrt{50 \times 10^3}} {\sqrt{2 \times 5 \times 3}} \right)^2 \rightarrow L_{M} > 143.1 \mu H$$

计算出应用所需的最小磁化电感后，再计算其最大值，该值受固定最大副边占空比的限制。可以公式 (7) 来计算L_{M_MAX}：

$$L_{\text{M_MAX}} < \left( \frac {(D'_{\text{MAX}} \times \frac{1}{f_{SW}}) \times N_{PS} \times (V_{\text{OUT}} + V_F) \times \sqrt{f_{SW}}} {\sqrt{2 \times P_{OUT}}}\right)^2$$

带入值进行计算：

$$L_{\text{M_MAX}} < \left( \frac {(0.4 \times \frac{1}{50 \times 10^{3}}) \times 15 \times (5 + 0.1) \times \sqrt{50 \times 10^{3}}} {\sqrt{2 \times 5 \times 3}} \right)^2 \rightarrow L_{M} < 624.24 \mu H$$

通过计算可知，磁化电感必须在 143.1µH 和 624.24µH 之间。但L_M的取值还需要平衡 RMS 电流和变压器尺寸。因此建议使用L_M在最大计算值的 60% 至80% 之间的变压器，以实现全功率且不会限制副边占空比。在本例中，我们采用 400µH 的磁化电感。

变压器值确定之后，就可以采用公式 (9) 来计算峰值电流：

$$I_{PK} = \sqrt{\frac{2 \times P_{OUT}}{\eta \times L_{M} \times f_{SW}}} = \sqrt{\frac{2 \times 5 \times 3}{0.85 \times 400 \times 10^{-6} \times 50 \times 10^3}} = 1.328A$$

本应用的目的是设计超宽V_IN，因此确保高V_IN下的最小导通时间超过前沿消隐时间非常重要。消隐时间在第一个开关周期内，此时控制器的内部比较器关闭，以避免由于击穿而激活短路保护 (SCP)。

通过公式 (10) 来估算最小导通时间（t_ON）：

$$t_{ON} = I_{PK} \times \frac{L_{M}}{V_{IN}} = 1.328 \times \frac{400 \times 10^{-6}}{815} = 652\,ns > 380\,ns$$

根据这一步的计算，可知所选磁化电感适合本应用。

步骤 4：分流电阻计算

计算出峰值电流之后，再设计分流电阻以正确闭合峰值电流控制环路。

根据 MP023 数据手册，采样电流在最坏情况下的最小电压限值为 0.464V。通过公式 (11) 来计算分流电阻（R_SHUNT）：

$$R_{\text{SHUNT}} = \frac{V_{CS}}{I_{PK}} = \frac{0.464}{1.328} = 0.35 \Omega$$

选择能够承受自身功耗的分流电阻，然后通过公式 (12) 来估算原边 RMS 电流：

$$I_{\text{P_RMS}} = I_{PK} \times \sqrt{\frac{D}{3}} = I_{PK} \times \sqrt{\left(\frac{I_{PK} \times L_{M} \times f_{SW}}{V_{IN}}\right) \div 3} = 1.328 \times \sqrt{\left(\frac{1.328 \times 400 \times 10^{-6} \times 50 \times 10^{3}}{90}\right) \div 3} = 0.417A$$

在本例中，功耗约为 61mW。

步骤 5：原边 MOSFET 计算

这一步用于为应用选择合适的原边 MOSFET。计算出最大峰值电流和 RMS 电流后，利用公式 (13) 来计算 MOSFET的最大耐受电压：

$$V_{\text{DS_MAX}} = (V_{\text{IN_MAX}} + V_w + 20\% \times \text{Margin}) = (815 + 76.5) \times 1.2 = 1070V$$

在本例中，所需原边 MOSFET的最大反向电压应为 1200V。

步骤 6：整流器 MOSFET 计算

与原边 MOSFET 计算类似，同步整流器的最大反向电压可以通过公式 (14) 来估算：

$$V_{\text{DS_MAX}} = V_{OUT} + \frac{V_{IN_{\text{MAX}}}}{n} + 40\% \times \text{Margin} = \left(5 + \frac{815}{15}\right) \times 1.4 = 83V$$

可以得知，本例所需的整流器 MOSFET最大反向电压应为 120V 至 150V。

副边 RMS 电流对于选择最佳整流器 MOSFET 也很重要。利用公式 (15) 来计算副边 RMS 电流（I_{S_RMS}）：

$$I_{\text{S_RMS}} = I_{\text{PK_S}} \times \sqrt{\frac{D'}{3}} = I_{PK} \times n \sqrt{\frac{D'}{3}} = 1.328 \times 15 \times \sqrt{\frac{0.4}{3}} = 7.27A$$

根据计算结果可知，本应用需要具有低导通电阻（R_DS(ON)）的整流器 MOSFET。

步骤 7：变压器设计

选择变压器需要考虑多种因素，例如磁芯材料和磁芯形状。对于本例所需的输出功率水平和输入电压而言，采用EF20 (E20/10/6) 在尺寸和有效面积方面都较为合适。

该变压器的原边匝数（N_P）可以通过公式（16）来估算：

$$N_P = \frac{L_M \times I_{PK}}{B_{MAX} \times A_E} = \frac{400 \times 10^{-6} \times 1.328}{0.275 \times 32.1 \times 10^{-6}} \approx 60$$

由于 f_SW 为 50kHz，因此N27 和 N97等磁芯材料可用于实现高达 0.3T 的最大磁通密度。为了以最低的原边匝数实现选定的匝数比，我们选择 0.275T。

N_P确定以后，就可以使用公式 (17) 计算出副边匝数（N_S）：

$$N_S = \frac{N_P}{n} = \frac{60}{15} \approx 4$$

然后选择 IC 的电源电压（V_CC），并通过公式 (18) 来估算辅助绕组匝数（N_AUX）：

$$N_{AUX} = \left(V_{CC} + 0.6\right) \times \frac{N_S}{V_{OUT}} = \left(12 + 0.6\right) \times \frac{4}{5} \approx 10$$

最后得到的变压器匝数比为：N_P:N_S:N_AUX = 60:4:10。

最终设计

所有重要元件值都计算出来之后，可以得到最终的电路设计如图 5所示。

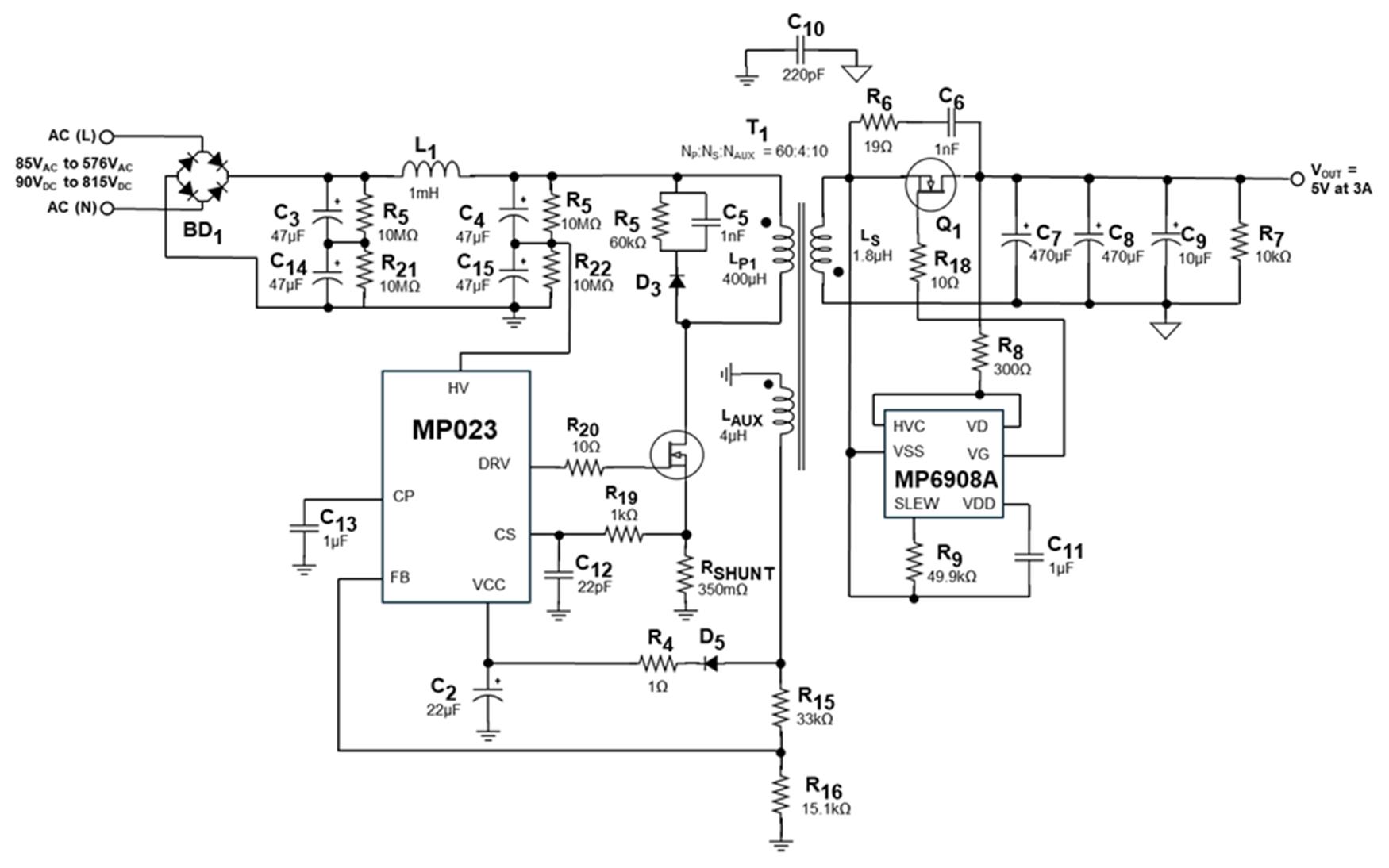
图 4：最终设计电路原理图

实验结果

为了验证上述计算，我们搭建出一个具有超宽输入电压范围的反激式变压器原型（见图 5）。

图 5：具有超宽输入电压范围的反激式变换器原型（无输入滤波器的 PCB）

该原型没有配置输入滤波器，这样可以使PCB更加灵活，它可以插入配置了不同输入滤波元件的另一个 PCB。

图 6 显示了变换器在最小电压下的验证结果。蓝色迹线代表原边 MOSFET 的漏源电压（V_DS），粉色迹线代表通过分流电阻采样得到的原边电流。

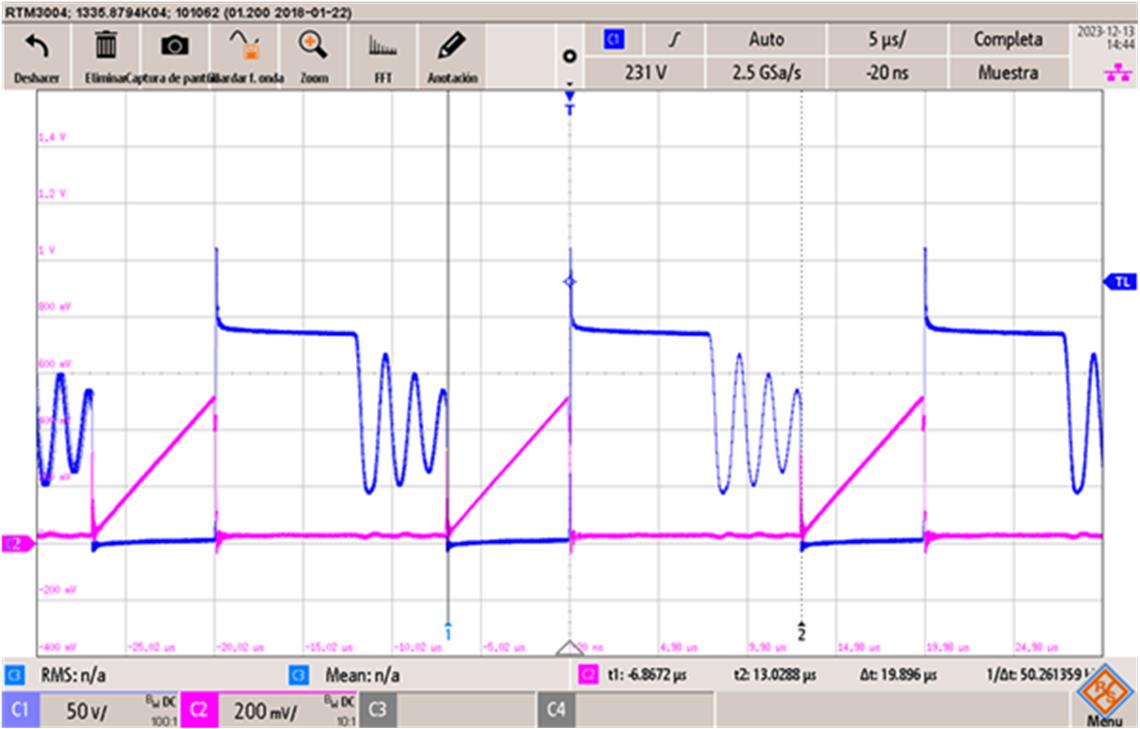
图 6：最小输入电压下的变换器验证结果

图 7 显示了最大电压下的变换器验证结果。蓝色轨迹代表原边 MOSFET 的漏源电压（V_DS）。

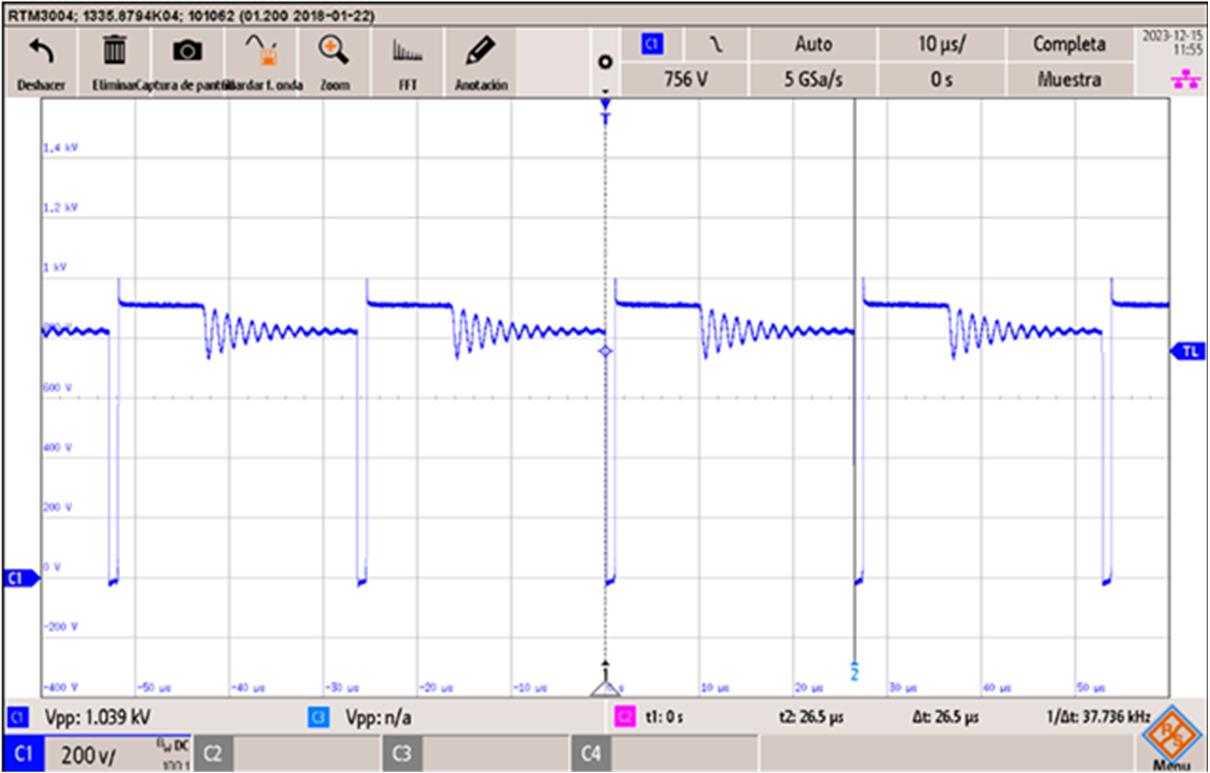
图 7：最大输入电压下的变换器验证结果

图 8 显示了本设计在不同输入电压下的效率验证结果。

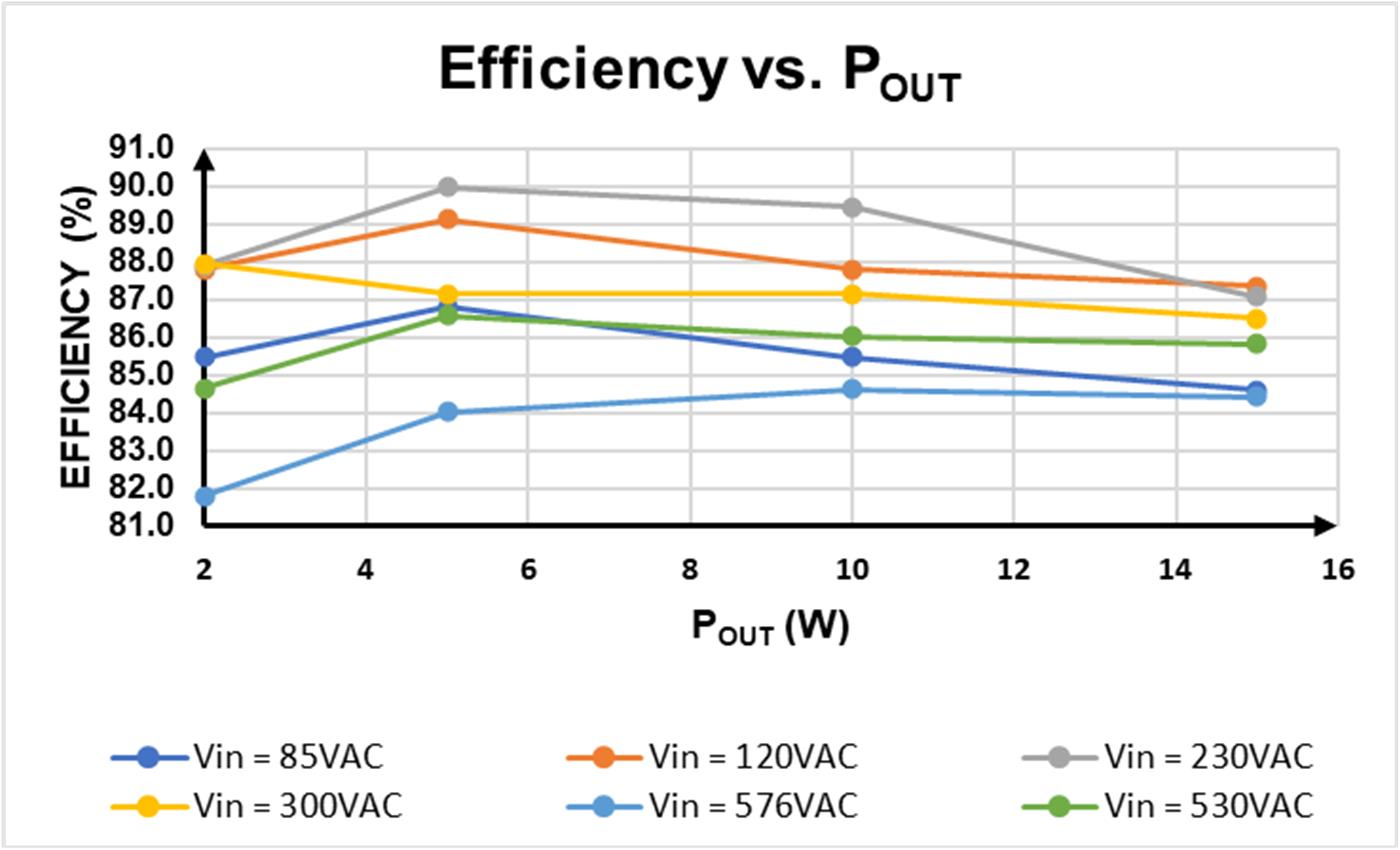
图 8：效率验证结果

如上图所示，由于副边采用了同步整流，变换器的效率相当高。此外，采用具有相对较低栅极电荷电容的原边 MOSFET 还可以降低高V_IN下的开关损耗。

结语

在需要三相输入的众多工业应用中，具有宽V_IN范围的反激式变换器非常有用。本文提供了一系列简单步骤，可通过MP023优化反激式变换器的设计。这些步骤包括了计算所需的匝数比、磁化电感和分流电阻，还包括选择关键参数以优化原边和副边 MOSFET 的设计。文中同时提供了设计验证结果，以证明本文所述方法的一致性和可行性。

除了 MP023 之外，MPS 还提供多款具有原边调节功能的反激式变换器。立即了解 MPS 强大的产品组合，找到满足您设计需求的解决方案。