Rectifiers, also known as AC-DC converters, are crucial components in modern power electronic systems, as they convert AC power into DC power. The suitability of these converters for a specific application is determined by several performance characteristics. It is essential to evaluate several significant performance characteristics, such as input current harmonic distortion, output ripple voltage, rectifier efficiency, and power factor, to assess the performance of AC-DC converters. Electrical engineers designing and evaluating AC-DC converters for different applications must have a comprehensive understanding of these characteristics.

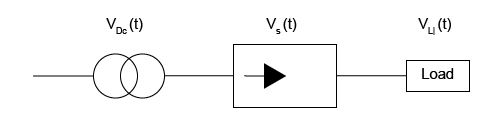
Figure 1: Generic scheme of a rectifier

The generic scheme of a rectifier is shown in figure above, where:

v_p(t) – transformer time-dependent primary voltage

v_s(t) – transformer time-dependent secondary voltage

v_L(t) – a time-dependent voltage at the output of the rectifier (on the load)

The DC voltage on the load is the average over the period T of the output voltage of the rectifier:

$$V_{DC} = \frac{1}{T} \int_0^T v_L(t) \, dt$$

The RMS voltage on the load can be calculated using the following equation:

$$V_L = \sqrt{\frac{1}{T} \int_0^T v_L^2(t) \, dt}$$

The ratio of the two voltages is the Form Factor (FF):

$$FF=\frac{V_L}{V_{DC}}$$

Let’s assume that the load itself is an ideal resistance. If so, the following currents can be determined:

$$i_L(t)=\frac{V_L(t)}{R_L}$$ $$I_{DC}=\frac{V_{DC}}{R_L}$$ $$I_L=\frac{V_L}{R_L}$$

The rectification ratio (η), also known as rectification efficiency, is expressed by:

$$η=\frac{P_{DC}}{P_L+P_D}$$

In the last equation, P_D represents the losses in the rectifier (R_D is the equivalent resistance of the rectifier). From the previous equations, we get:

$$\eta = \frac{V_{DC} \cdot I_{DC}}{V_L \cdot I_L + R_D \cdot I_L^2} = \frac{V_{DC}^2}{V_L^2} \cdot \frac{1}{1 + \frac{R_D}{R_L}}$$

If the switches are ideal (with no losses, that is R_D = 0), the rectification efficiency is equal to:

$$\eta = \frac{V_{DC}^2}{V_L^2} = \frac{1}{FF^2}$$

The Ripple Factor (RF) represents the smoothness of the voltage waveform at the output of the rectifier. The RF is defined as the ratio of the effective AC component of the load voltage versus the DC voltage:

$$RF = \sqrt{\frac{V_L^2 - V_{DC}^2}{V_{DC}}} = \sqrt{FF^2 - 1}$$

One of the parameters used to define the characteristics of the transformer is the Transformer Utilization Factor (TUF):

$$TUF=\frac{P_{DC}}{S_T}$$

where S_T represents transformer rated (apparent) power.

The Displacement Power Factor is defined as:

$$DPF=\cos{\Phi_1}$$

where Φ₁ represents the input displacement angle, i.e. the angular displacement between the fundamental components of the AC line current and associated line to neutral voltage.