Introduction to Equivalent Circuit Models (ECMs)

Basic Concept of ECMs

A class of models called equivalent circuit models (ECMs) is used to simulate the electrical dynamics of batteries. ECMs use electrical components like resistors, capacitors, and voltage sources to simulate the electrical response of the battery, as opposed to electrochemical models, which are based on chemical reactions and processes occurring within the battery. When compared to electrochemical models, these models are typically simpler to comprehend, use, and they require a lot less computational power.

Typically, a combination of voltage sources, resistors, and capacitors is used in ECMs to mimic the battery.

The voltage sources take into consideration the battery's SOC-dependent open-circuit voltage. While the capacitors simulate the battery's transient behavior, the resistors capture internal resistance and polarization losses.

Applications of ECMs

Battery Management Systems: ECMs are commonly integrated into Battery Management Systems to estimate critical parameters such as State of Charge (SOC), State of Health (SOH), and available power. Their simplicity and computational efficiency render them well-suited for real-time applications where swift and accurate assessment of battery performance is essential.

Electric Vehicle Control Systems: ECMs play a pivotal role in developing control strategies for electric vehicles, this encompasses aspects like energy management and regenerative braking systems. These models are instrumental in estimating the current state of the battery and predicting its future performance, contributing to safe and efficient vehicle operation.

Power System Simulations: In the realm of power system analysis and simulations, ECMs can effectively emulate the behavior of battery energy storage systems. They prove particularly valuable in grid simulations, where the intricate nuances of electrochemistry are not imperative, and the focus is primarily on system-level performance.

Battery Charger Design: ECMs are frequently employed in the design of battery chargers to optimize charging profiles. By using these models, charger designs can be tailored to enhance battery performance and extend longevity.

ECMs are characterized by their ability to strike a balance between model fidelity and computational efficiency. They excel in applications necessitating real-time simulation or control, where the intricate details provided by full electrochemical models may not be essential. However, it's important to note that ECMs may have limitations in accurately predicting long-term battery behavior, particularly when faced with variable environmental or operational conditions.

Simple ECMs

Simple Battery Model

The Simple Battery Model is one of the most basic and popular ECMs. In this approach, a series connection between a voltage source and a resistor represents the battery. The potential difference across the battery terminals when there is no current flowing is represented by the voltage source, often known as the open-circuit voltage (OCV). The series resistor (Ro) measures the internal resistance of the battery and is responsible for the sudden voltage drop that happens when current begins to flow through the battery. Due to the internal resistance effect, the Simple Battery Model only records the open-circuit voltage and the resistive voltage drop inside the battery. The model does not capture the rapid dynamics of the battery but is appropriate for making straightforward, immediate predictions of battery state in electronics systems.

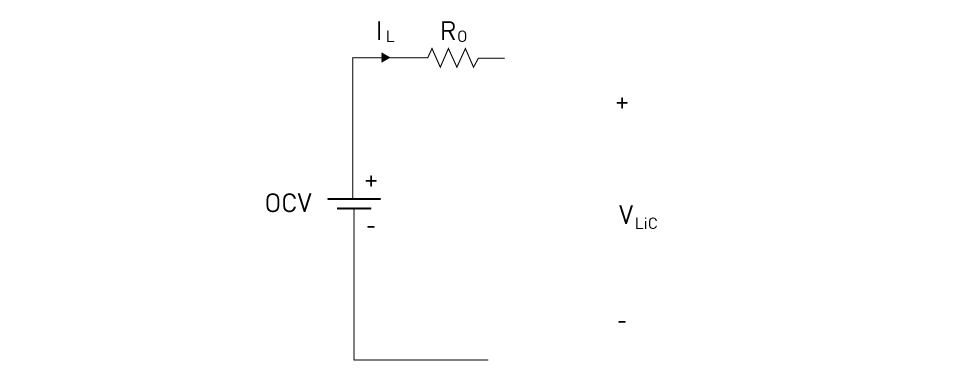
Figure 4: Battery ECM Simple Battery Model

Single R-C Pair Thevenin Model

The Single R-C Pair Thevenin Model is a variation of the Thevenin model, and it incorporates a single resistor-capacitor (RC) pair connected in series with the open-circuit voltage (OCV) source. Much like the conventional Thevenin model, the OCV source symbolizes the battery's no-load voltage, while the series resistor (Ro) signifies its internal resistance. In this model, the RC pair, consisting of a capacitor (Cp) and resistor (Rp) is introduced to capture polarization effects and transient battery behavior.

Within this model, the voltage across the capacitor in the RC pair undergoes gradual buildup. This behavior symbolizes the slower dynamics observed in batteries, including phenomena like the recovery effect. Although this model is computationally efficient and well-suited for real-time applications, it provides a simplified approximation of battery dynamics. Its inherent simplicity can be advantageous in control applications where rapid computational speed takes precedence over highly detailed modeling, making it a practical choice for scenarios where computational efficiency is paramount.

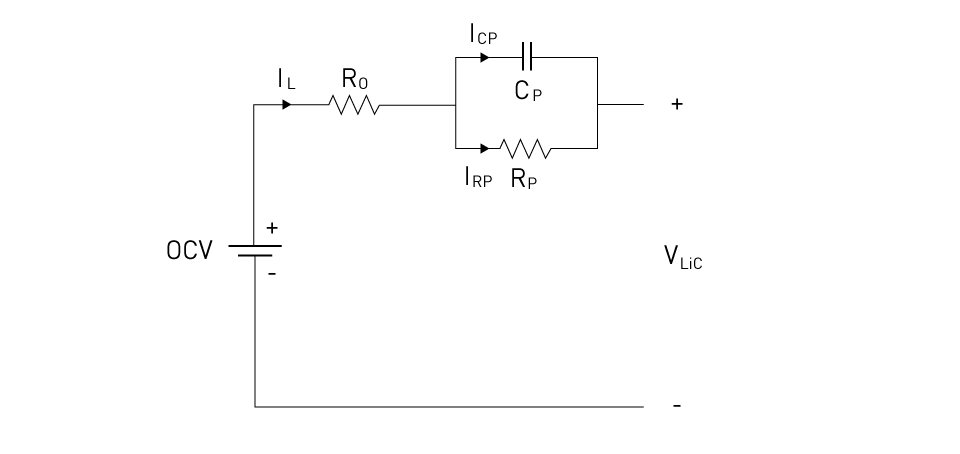
Figure 5: Battery ECM Thevenin Model with single RC pair

Complex ECMs

Multiple R-C Pairs Thevenin Model

As we explore more complex Electrochemical Models (ECMs), one noteworthy approach involves the incorporation of Multiple R-C Pairs. In contrast to the single R-C pair model, which relies on a solitary resistor-capacitor (RC) network to depict battery dynamics, the multiple R-C pairs model (Cpn and Rpn) introduces numerous RC networks operating in parallel. This methodology takes into account diverse time constants (determined by the product of Cp and Rp) associated with various electrochemical processes within the battery. Individual RC networks capture a distinct dynamic behavior, thereby offering a more comprehensive portrayal of how the battery responds to changes in load and charge.

In practical implementation, each RC pair in the model signifies a different time-scale of polarization effects. This strategic configuration ensures that the model can effectively simulate both rapid and gradual transient phenomena encountered in the battery. It's important to note that while the multiple R-C pairs model demands more computational resources compared to its simpler counterparts, it delivers heightened accuracy. This makes it particularly well-suited for applications where detailed simulations are paramount, such as in battery management systems and optimization algorithms, where precision is critical for informed decision-making and performance enhancement.

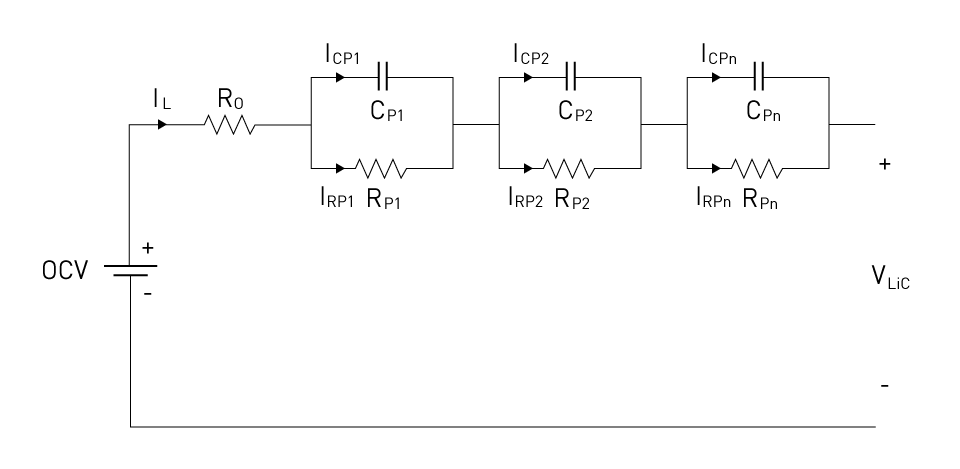
Figure 6: Battery ECM Thevenin Model with multiple RC pairs

Diffusion Models

Diffusion models are a crucial component of sophisticated ECMs. The diffusion of lithium ions in the electrodes is a key mass transport phenomenon within the battery that is primarily represented using diffusion models. Warburg impedance modeling is a popular method for modeling diffusion in ECMs:

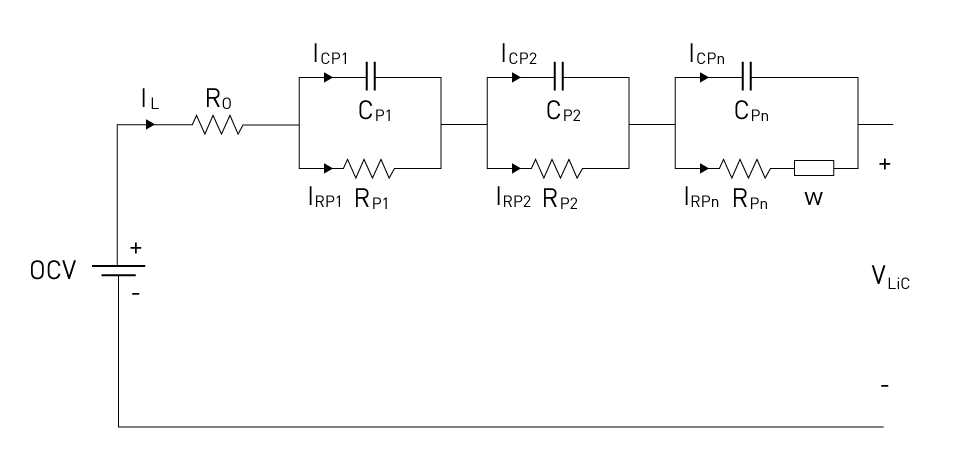
Figure 7: Battery ECM multiple RC pairs with Warburg impedance

One of the RC pairs in this model has a Warburg impedance added to it. The semi-infinite diffusion of ions through the electrolyte and electrodes is represented by the Warburg impedance. This component is frequency-dependent and accounts for the polarization losses resulting from diffusion that takes place at lower frequencies or over longer periods.

By integrating diffusion models into Electrochemical Models (ECMs), it becomes feasible to replicate and analyze the influence of ion diffusion on the battery's performance, particularly with regard to voltage response and State of Charge (SOC). This capability facilitates a more accurate prediction of battery performance across a spectrum of load conditions.

It's noteworthy that while complex ECMs that encompass multiple R-C pairs and diffusion models impose higher computational demands in comparison to simpler ECMs, they deliver a more intricate and precise depiction of battery behavior. This elevated level of detail renders them exceptionally valuable in applications where comprehensive and high-fidelity modeling is imperative. Such applications encompass the design and optimization of battery systems tailored for electric vehicles, grid storage solutions, and other demanding, high-performance scenarios.

State-Space Representation of ECMs

Conversion of ECM to State-Space Form

When modeling a physical system mathematically, the state-space representation uses a set of first-order differential equations rather than the system's defining differential equation, which could have multiple orders and be difficult to handle. Converting ECMs to state-space form in the context of battery modeling is a potent method for examining the dynamic behavior of the system.

One must derive the mathematical relationships that characterize the interactions between the various components (resistors, capacitors, voltage sources, etc.) within the circuit in order to transform an ECM into a state-space representation. The differential equations are commonly constructed using Kirchhoff's current and voltage rules. The state equations and the output equation are always present in the state-space representation.

Let's take an ECM consisting of a resistor and a capacitor in series connection:

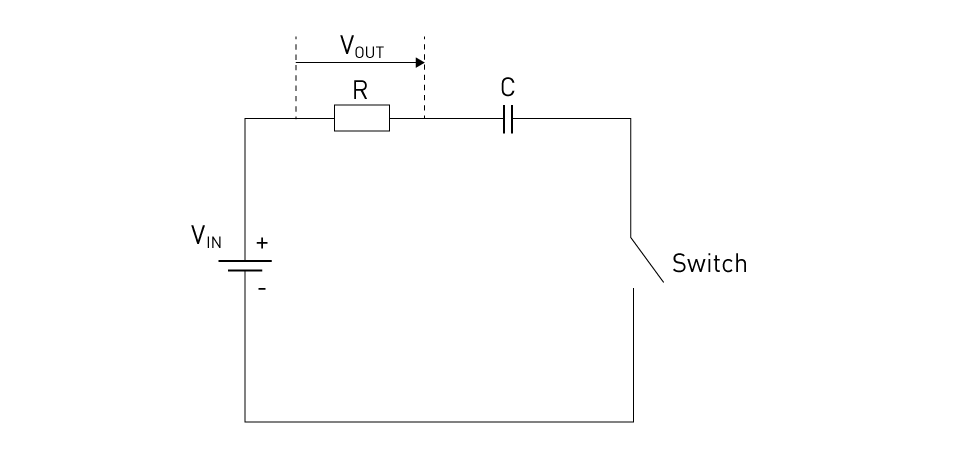
Figure 8: Simple RC circuit

The number of energy storage devices (capacitors and inductors) present in an electronic circuit is equal to the number of state equations. In our case, there is only one capacitor, and Kirchoff's rules are used to get the voltage equation for it:

$$\frac{dV_c}{dt} = \frac{1}{RC} (V_{\text{in}} - V_c)$$

The output equation we choose is the voltage of the resistor:

$$V_{\text{out}} = V_{\text{in}} - RC \cdot \frac{dV_c}{dt}$$

Here, V_in is the input voltage, V_out is the output voltage, C is the capacitance, V_c is the voltage across the capacitor (also known as the "state variable"), R is the resistance, and C is the capacitance.

This set of equations can then be expressed in matrix form as:

$$\frac{dX}{dt} = AX + BU$$ $$Y=CX+DU$$

Where X represents the state vector [V_c], U is the input vector [V_in], Y is the output vector [V_out], and A, B, C, and D are matrices derived from the ECM’s passive components. These vectors hold multiple input, output, and state variables in more complex systems.

Applications in Control and Estimation

Once the state-space representation is derived, it proves exceptionally advantageous in the design of control systems and estimation algorithms tailored for batteries.

BMS Control: The state-space model plays a pivotal role in shaping controllers for Battery Management Systems (BMS). Controllers leverage the model to gauge critical battery states such as State of Charge (SOC), State of Health (SOH), and others. Based on these estimates, decisions regarding charging rates, discharging rates, balancing operations, and other pivotal aspects are made to optimize battery performance.

State Estimation: Utilizing state-space models, advanced techniques like Kalman filters and other state estimation methods can deduce internal battery states that aren't directly measurable. This capability is vital for predicting SOC and SOH, both of which are paramount for ensuring the safe and efficient operation of batteries.

Optimization: State-space models serve as a linchpin in optimization algorithms aimed at pinpointing the most advantageous operating points for batteries. This encompasses identifying optimal charging and discharging schedules that maximize battery life and efficiency.

Simulation and Analysis: The state-space representation opens the door to simulating the dynamic behavior of batteries under diverse conditions. This facilitates comprehensive performance analysis and validation, enabling engineers and researchers to gain insights into how batteries perform in various scenarios and under different parameters.

Battery Thermal Models

Basic Concept

Battery Thermal Models (BTMs) are formulated to delve into the thermal characteristics of batteries with a particular focus on temperature fluctuations and heat generation during charging and discharging processes. The production of heat within batteries stems from various factors, including internal resistance, electrochemical reactions, cell imbalances, and the entropy change accompanying these reactions. The management of a battery's thermal behavior holds paramount importance as it has a direct impact on its performance, efficiency, safety, and longevity.

A fundamental Battery Thermal Model often comprises a thermal equivalent circuit where heat generation is represented as a current source. The thermal resistance of materials is depicted as resistors and heat capacity is symbolized by capacitors. In such models, the state variables typically encompass temperatures at various points within the battery. To illustrate, consider a simplified thermal equivalent circuit for a cylindrical-shaped battery, where heat is transferred in the radial direction:

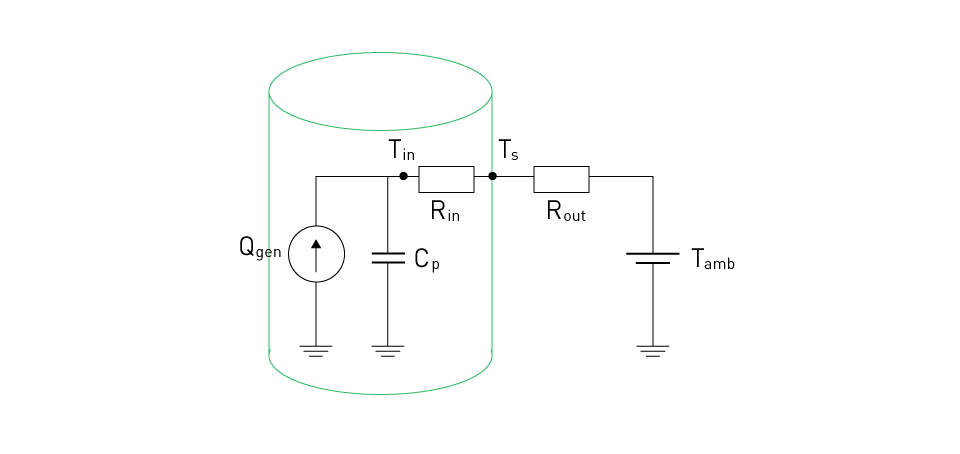
Figure 9: Simple thermal equivalent circuit of a cylindrical battery

Q_gen serves as the heat generation source within the battery, acting like a current source that propels current through the other components. C_p represents the internal thermal capacitance of the battery. R_in stands for the thermal resistance from the heat source to the battery's surface, dictating how heat flows within the battery. R_out signifies the thermal resistance from the battery's surface to the surrounding environment, typically considering convective heat transfer when air is the surrounding medium. T_amb represents the ambient temperature surrounding the battery, which is modeled as a voltage source. This thermal model enables the estimation of both the internal temperature (T_in) and the surface temperature (T_s) of the battery.

Assumptions and Simplifications

To streamline calculations, certain common simplifications and assumptions are made, they include:

Homogeneity: This is assumed to be homogenous, meaning that the materials within the battery are considered to be uniform in their properties throughout.

Constant Properties: Thermal properties of materials like specific heat and thermal conductivity are frequently presumed to remain constant despite the possibility of variations in temperature. These simplifications aim to make BTMs more computationally efficient while providing reasonably accurate results.

Quasi-Steady State: Occasionally, it's assumed that temperatures change at a slow enough rate that the system can be treated as a nearly steady-state. This simplifies the equations governing transient heat conduction.

One-Dimensional Heat Transfer: In certain models, heat transfer is assumed to occur primarily in one dimension, usually in the radial direction. This simplification is employed to reduce model complexity.

Neglecting Convection and Radiation: Frequently, only conductive heat transfer is taken into account within the battery with the effects of convection and radiation considered minimal and thus disregarded.

Applications and Limitations

Applications:

Performance Analysis: BTMs find application in assessing how fluctuations in temperature impact battery performance, encompassing factors such as capacity, power output, and efficiency.

Thermal Management System Design: BTMs play a pivotal role in the development of thermal management systems for batteries. These systems are particularly crucial in electric vehicles, and they include cooling and heating mechanisms. In instances where excessively low temperatures can result in reduced battery capacity and compromised charging/discharging performance, the thermal management system intervenes by heating the battery to attain the optimal operational temperature. Software tools like MATLAB and SIMULINK facilitate comprehensive simulations of these thermal management system designs.

Safety Analysis: Through the prediction of temperature profiles, BTMs contribute to the assessment of battery safety. This proves especially significant in averting scenarios of thermal runaway, ensuring the safe operation of batteries.

Lifetime Prediction: A profound understanding of thermal behavior aids in predicting the lifespan of batteries. Elevated temperatures accelerate degradation mechanisms, and this knowledge proves invaluable in forecasting the durability of batteries over time.

Limitations:

Accuracy: The accuracy of BTMs can be constrained by the simplifications and presumptions utilized in the models, especially when forecasting the temperature distributions within the battery.

Computational Complexity: Complex models that don't simplify much can be more computationally demanding, which makes them less useful for real-time applications.

Material Property Variations: Most BTMs do not take into consideration changes in material properties with Temperature, which can influence the model's accuracy.