Introduction to Electrochemical Modeling

Basic Concepts of Electrochemistry

The interplay between chemical and electrical processes is the subject of the field of chemistry known as electrochemistry. It focuses on the phenomena that emerge from the motion of ions and electrons during chemical reactions that can either generate or consume electric energy.

Redox Reactions: The redox reaction, which involves the transfer of electrons between two species is a key idea in electrochemistry. One species is reduced (gains electrons) and the other is oxidized (loses electrons) in redox reactions.

Electrochemical Cells: These are gadgets that utilize redox processes to change chemical energy into electrical energy. Anode and cathode electrodes, along with an electrolyte, make up an electrochemical cell. Oxidation takes place at the anode, and reduction happens at the cathode. Ions can move between the electrodes thanks to the electrolyte.

Electrode Potential: It speaks about an electrode's capacity to lose or gain electrons. Cell potential, also referred to as electromotive force (EMF) is the force that propels the flow of electrons across an external circuit due to the difference in electrode potentials between the cathode and anode.

Nernst Equation: This equation connects the cell potential to the reactant and product concentrations at any given time. It is essential for comprehending how electrochemical cells discharge and charge.

The Role of Electrochemical Reactions in Batteries

Batteries are electrochemical cells meticulously engineered to convert chemical energy into electrical energy, a versatile source of power for various devices. Their operation hinges on electrochemical reactions unfolding at the electrodes.

Energy Storage and Release: When a battery undergoes charging, it harnesses external electrical energy to drive redox reactions in the reverse direction. This process stores energy by forming and preserving chemical bonds. During the discharge process, these reactions occur spontaneously, resulting in the conversion of stored chemical energy back into electrical energy, which powers devices.

Role of the Electrolyte: Within batteries, the electrolyte serves as a conduit for the movement of ions between the anode and cathode. This ionic mobility is essential for preserving charge neutrality while electrons traverse the external circuit linked to the battery terminals. The electrolyte acts as the bridge facilitating this ion transfer.

Battery Degradation: Over time, the repetitive cycles of charging and discharging inflict physical and chemical transformations upon the battery materials. These alterations can manifest as a decline in capacity, an increase in internal resistance, and ultimately, the failure of the battery. A profound comprehension of the electrochemical reactions and their kinetics is imperative for investigating and mitigating battery degradation, which is a pivotal aspect of battery technology and sustainability.

Single Particle Model (SPM)

The Single-Particle Model (SPM) is a popular electrochemical model for investigating and simulating lithium-ion battery performance. SPM maintains fundamental characteristics that are crucial for many applications while streamlining the intricate electrochemical processes occurring inside a battery to make simulations computationally efficient.

Assumptions and Simplifications

Uniform Electrolyte Concentration: It is assumed in the SPM that the electrolyte concentration is homogeneous across the cell in terms of space. This suggests that the electrolyte content simply varies with time and does not alter in relation to place.

Spherical Active Material Particles: The model assumes that the active material particles within the electrodes have a spherical shape. This simplification helps streamline the geometry for solving complex diffusion equations, making the mathematical modeling more manageable.

Single Particle Representation: Instead of considering spatial variations within the electrodes, the SPM approach represents all the active material in each electrode (both cathode and anode) as a single spherical particle. This simplification significantly reduces the computational complexity compared to models that account for spatial variations, making it a more efficient way to simulate battery behavior.

Constant Solid Phase Diffusivity: The model assumes that the diffusion coefficient within the solid phase of the electrode material remains constant. This simplifies the modeling of ion movement within the solid material and allows for a more straightforward mathematical treatment.

The single-particle model can be visualized as follows:

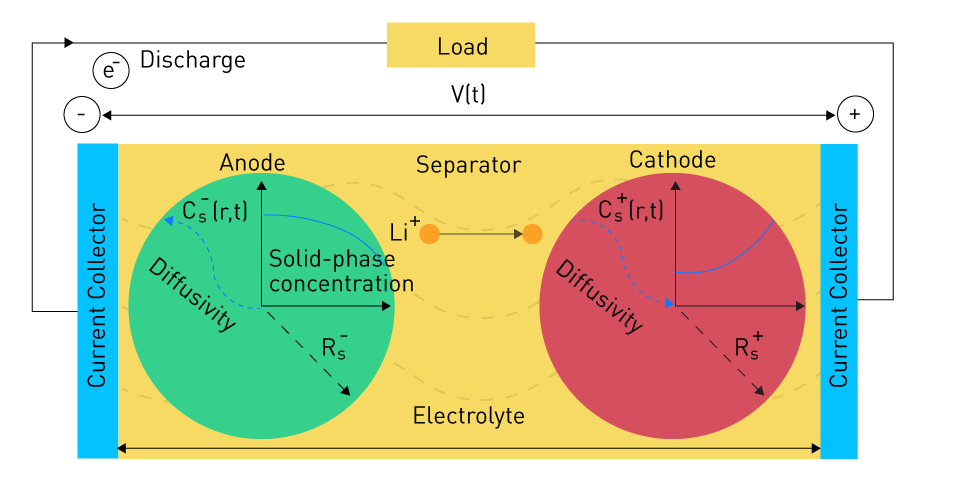
Figure 1: Single Particle Model (SPM)

In this simplified model, both the anode and cathode are represented as a single solid particle. It captures the phenomenon of decreasing Li+ ion concentration as you move away from the center along the "r" axis of this single solid particle.

Governing Equations

Solid Phase Diffusion Equation: Fick's second law of diffusion is used to simulate the movement of lithium ions within the particles of solid active material. With time and radial position inside the particles, the concentration of lithium ions in the solid phase changes.

$$\frac{\partial c_s}{\partial t} = \frac{D_s}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial c_s}{\partial r} \right)$$

Where,

t equates to time

r represents the radial distance from the center of the single particle model

C_s equates to concentration of lithium ions at “r” distance from the center of the single particle model

∂C_s/∂t is the rate of change of the concentration of lithium ions in the solid state with respect to time (time derivative of the concentration).

D_s represents the diffusion coefficient of Li ions in the solid phase

Overpotential: The extra voltage or energy needed to propel a desired electrochemical reaction at the battery's electrodes is referred to as overpotential. It is the difference between the actual applied voltage and the voltage that would be necessary according to thermodynamics for a given electrochemical reaction to take place. Overpotential promotes undesirable battery processes such as lithium plating, where lithium ions are ejected from the electrolyte and accumulate on the surface of the anode as a result of charging the cell at a high current, permanently impairing battery performance. The following is the overpotential equation:

$$\eta = F^{-1}\left(\phi_{s,j} - \phi_{e,j}\right) - U\left(c_s\right)$$

Where,

1/F represents the Faraday constant

Φ_s,j represents the solid phase potential and j is either an anode or cathode

Φ_{e ,j} represents the electrolyte phase potential and j represents either anode or cathode

U(Cs) represents the Open Circuit Voltage

Electrode Voltage Equations: The voltage of each electrode depends on the amount of lithium present in the particles of the active material. Usually determined empirically and incorporated into the model are the open-circuit voltage (OCV) relations.

Overall Cell Voltage: Calculating the overall cell voltage involves deducting the anode voltage from the cathode voltage in the solid phase and taking into account overpotentials brought on by reaction kinetics and ohmic losses in the electrolyte. The total cell voltage is obtained by converting the electrolyte phase potential into an internal resistance with the formula: internal resistor Φ_e,p - Φ_e,n = I*Rcell where I is the electric current flowing through the battery.

$$\text{Cell Voltage} = \left(\phi_{s,p} - \phi_{s,n}\right) - I \cdot R_{\text{cell}}$$

Applications and Limitations

Applications: In terms of applications, the Single Particle Model (SPM) finds widespread use in examining the fundamental behavior of lithium-ion batteries, particularly in the context of state of charge (SOC) estimation. Its simplicity lends itself well to computational efficiency, rendering it suitable for real-time applications like battery management systems.

Limitations: It's also essential to acknowledge its limitations. The SPM's simplifications lead to the omission of several critical phenomena, including electrolyte transport, concentration gradients within the electrolyte, and thermal effects. Consequently, its applicability may be limited in scenarios demanding high-fidelity simulations or applications where these omitted factors exert a substantial influence, such as in-depth thermal runaway analysis or comprehensive life-cycle assessments.

Pseudo-Two-Dimensional Model (P2D)

Regarding the Pseudo-Two-Dimensional Model (P2D), also recognized as the Newman model, it serves as a widely embraced electrochemical model for lithium-ion batteries. This model, unlike the SPM takes into consideration transport phenomena occurring in both the solid and electrolyte phases. It meticulously accounts for spatial variations spanning from the anode to the cathode and the radial variations occurring within active material particles.

Assumptions and Governing Equations

Spherical Active Material Particles: P2D makes the same assumption as SPM about the sphericalness of the active material particles.

Constant Solid Phase Diffusivity: The model presupposes that the solid phase's diffusion coefficient is constant.

No Velocity in Electrolyte Phase: P2D makes the assumption that the electrolyte phase has no velocity, meaning that the only mechanisms by which lithium ions are transported in the electrolyte are diffusion and migration.

Isothermal Conditions: Although thermal effects may be added, the model normally assumes isothermal conditions.

Governing Equations:

Solid Phase Diffusion. It is similar to the SPM model:

$$\frac{\partial c_s}{\partial t} = \frac{D_s}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial c_s}{\partial r} \right)$$

Overpotential is the same with the SPM model:

$$\eta = F^{-1}\left(\phi_s - \phi_e\right) - U\left(c_s\right)$$

Electrolyte Phase Diffusion:

$$\epsilon \frac{\partial c_e}{\partial t} = \frac{\partial}{\partial x} \left( D_e \epsilon \frac{\partial c_e}{\partial x} \right) - \left(1 - t_+\right) \frac{1}{F}$$

Where,

E represents the volume fraction of the region (positive, separator, negative) that is electrolyte

D_e represents the diffusion coefficient in the electrolyte phase

x is the distance across the cell

C_e represents the electrolyte concentration

∂C_e/∂t is equal to the rate of change of the concentration of lithium ions in the electrolyte with respect to time (time derivative of the concentration).

t+ represents the Transference Number

1/F represents the Faraday constant

Charge Transfer at The Solid-Electrolyte Interface:

$$a_{sj_n} = \frac{-I}{F} = 2k \left(c_s^{\text{surf}}, c_e\right) \sinh\left(\frac{F \eta}{2RT}\right)$$

a_s represents particle surface area

j_n represents the pore-wall flux density

I represents the current

k represents the Peucert constant

C_s^surf represents the ion concentration at the surface of solid particles

C_e represents the ion concentration in the electrolyte

F represents the Faraday constant

R represents the universal gas constant

T represents the temperature

The pseudo-two-dimensional model can be visualized as follows:

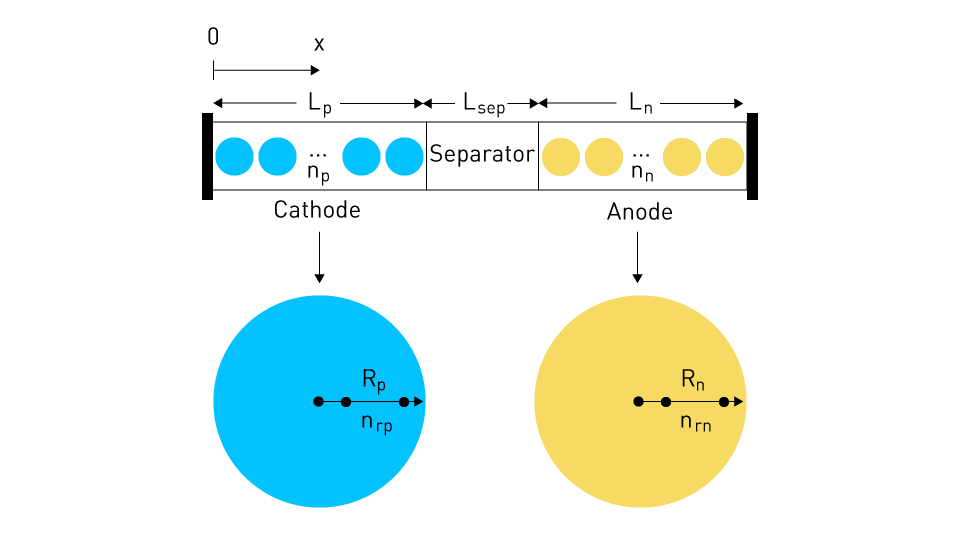
Figure 2: Pseudo-Two-Dimensional Model (P2D)

The single solid particles align themselves within the electrolyte phase, extending from the cathode to the anode, spanning a distance denoted as "x" from an arbitrary zero point. In this model, lithium-ion diffusion occurs along this axis within distinct regions, encompassing the cathode, separator, and anode. Additionally, diffusion occurs radially from the center point within each individual solid particle.

Numerical Solution Techniques

Discretization: The governing partial differential equations (PDEs) are typically subjected to discretization using either finite difference or finite volume methods. This process transforms them into a system of algebraic equations that can be readily analyzed and solved.

Time Stepping: Time integration is a crucial step in the modeling process. It involves employing either explicit or implicit methods to advance the simulation in time. Implicit methods are often favored for their inherent stability properties, particularly when dealing with complex dynamic systems.

Solvers: To solve the resulting nonlinear algebraic system at each time step, numerical techniques such as Newton's method or other nonlinear solvers are employed. These solvers are instrumental in obtaining solutions that accurately depict the evolving behavior of the system over time.

Applications and Limitations

Applications: The P2D model serves as a prevalent choice in the realm of lithium-ion battery design and optimization. It particularly shines when a comprehensive understanding of spatial concentration and potential distributions is essential. Its applications span diverse areas, encompassing cell design, state-of-charge estimation, thermal analysis, and degradation modeling.

Limitations: There are noteworthy limitations to consider. The P2D model is characterized by its complexity and computational demands, rendering it unsuitable for real-time applications, such as battery management systems (BMS), where rapid calculations are imperative. Furthermore, integrating factors like mechanical stress, aging effects, and parameters influenced by temperature variations can pose challenges when incorporating them into the P2D model.

Advanced Electrochemical Models

As battery technologies advance, the demand arises for models that can effectively capture the intricate interactions among various physical phenomena occurring within a cell. Advanced electrochemical models meet this demand by addressing the limitations inherent in simpler models like the Single Particle Model (SPM) and Pseudo-Two-Dimensional Model (P2D). These advanced models achieve this by incorporating additional physics or enhancing the precision of existing representations, facilitating more comprehensive and accurate simulations of battery behavior.

Multiphysics Models

Multiphysics models, by definition, account for multiple physical phenomena simultaneously. In the context of batteries, this typically encompasses electrochemical reactions, heat transfer, mechanical stress, and fluid dynamics.

Implementation: In terms of implementation, these models amalgamate the governing equations of various physical domains into a unified mathematical framework. For instance, a multiphysics model might interconnect electrochemical reactions with equations governing heat generation and transfer to comprehensively analyze a cell's thermal behavior. These models are often constructed using Finite Element Modeling (FEM) methods, operating in three-dimensional space, facilitated by Computer-Aided Design (CAD) software like COMSOL or ANSYS.

Applications: Regarding their applications, multiphysics models prove invaluable in the domain of design optimization, particularly in scenarios where the interplay between different physical phenomena holds paramount importance. Examples include analyzing thermal runaways, investigating short-circuits within batteries, assessing mechanical deformation caused by factors like swelling or crash impacts, studying overplating phenomena, or examining electrolyte flow in flow batteries. In such instances, multiphysics models provide a holistic understanding of complex interactions and enable the refinement of battery designs for enhanced safety and performance.

Thermal-Electrochemical Models

A specific kind of multiphysics model called a thermal-electrochemical model focuses on how heat generation and transfer within a battery are coupled with electrochemical reactions.

Implementation: By including the energy balance equation to account for heat generation owing to internal reactions, the Joule heating due to ion transport, and the exchange of heat with the environment, these models expand the electrochemical models.

Applications: The design of thermal management systems for batteries, forecasting thermal runaway situations, and examining the impact of operating conditions on temperature distributions within a cell all require the use of thermal-electrochemical models. The following image shows a simulation of a thermal-electrochemical battery pack in a 3D environment:

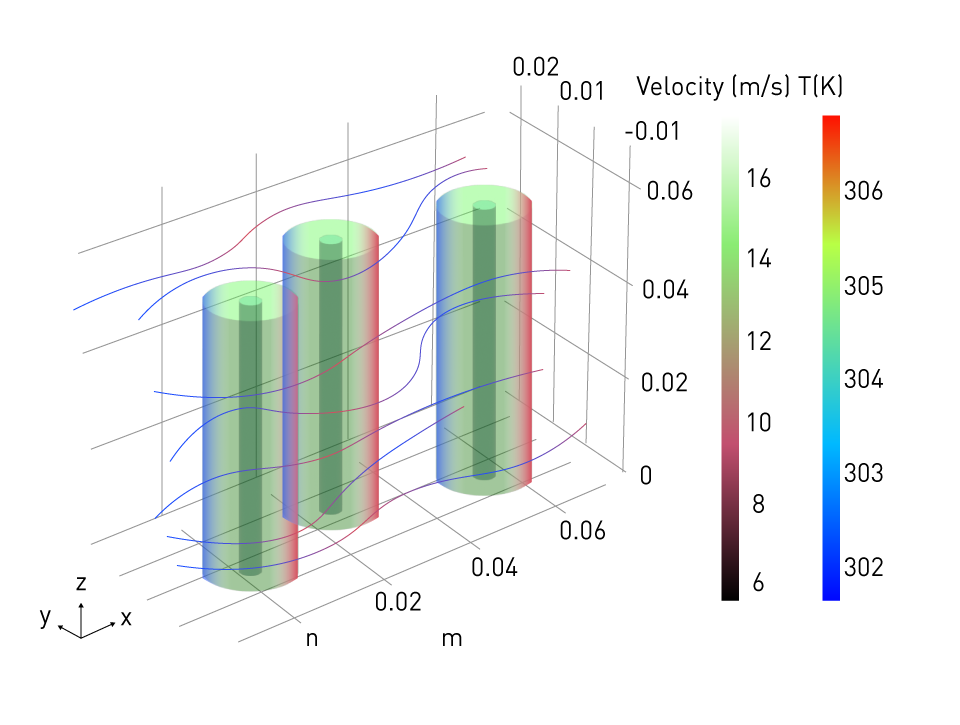
Figure 3: Thermal-electrochemical simulation of a battery pack

Simulation plays a crucial role in gaining insights into the temperature distribution within each battery cell and identifying the locations where hotspots are generated. Additionally, it facilitates the design of an effective cooling system that can regulate the battery's temperature within the desired range.

Particle Size Distribution Models

Regarding Particle Size Distribution (PSD) models, traditional electrochemical models often make the simplifying assumption of a uniform active material particle size. However, in reality, the sizes of these particles are distributed across a range. PSD models are designed to account for this distribution.

Implementation: The PSD often typically employs population balance equations to represent the distribution of particle sizes. These equations enable the consideration of variations in electrochemical behavior across particles of different sizes.

Applications: The applications of PSD models are particularly valuable for understanding capacity fade and performance degradation in batteries. This is because active material particles often undergo structural changes over time, leading to alterations in their size distribution. By incorporating these size variations, PSD models provide a more accurate representation of battery behavior, enabling researchers to study and mitigate the effects of capacity fade and performance decline over the battery's lifespan.