Introduction to Analog Control Systems

Analog control systems are the core of control engineering, providing reliable and robust methods for managing the behavior of dynamic systems. These systems are characterized by their use of analog controllers and devices to control processes in real-time, and they operate by employing continuous signals. Engineers working in a range of applications, from consumer electronics to industrial automation, must comprehend the fundamentals of analog control.

Fundamentals of Analog Control Systems

Continuous signals are used by an analog control system to monitor and adjust a system's behavior. Analog control systems employ continuous electrical signals to carry out control activities, in contrast to digital control systems that use discrete signals and digital processors. Analog sensors, operational amplifiers (op-amps), inductors, resistors, and capacitors are frequently used in the implementation of these systems.

Components of Analog Control Systems:

Sensors: Measure physical quantities (such as temperature, pressure, and speed) and convert them into analog electrical signals.

Actuators: Execute control actions based on analog signals, such as modifying valve position or motor speed.

Controllers: Analyze sensor analog signals to generate the proper actuator control signals. Op-amp circuits configured for proportional, integral, or derivative actions are examples of common analog controllers.

Continuous Signals:

Nature: Continuous signals, which are used in analog control systems, can have any value within a specified range and vary smoothly over time.

Advantages: High resolution and accuracy are offered by continuous signals, which is advantageous for applications requiring precise control.

Operation of Analog Control Systems

Analog control systems operate by constantly monitoring a process's output and adjusting the input to preserve the intended system behavior. This constant monitoring and adjustment are usually accomplished by feedback loops.

Feedback Loops:

Principle: A feedback loop lowers the error between the intended and actual outputs by feeding the system's output signal back into the input.

Components: A typical feedback loop includes an actuator (which adjusts the system based on the controller's output), a comparator (which compares the desired setpoint to the actual output), a controller (which handles the error signal), and a sensor.

Figure 1: Control system with feedback

Error Signal:

Definition: The error signal indicates the difference between the desired setpoint and the system's actual output.

Purpose: The control action is driven by the error signal. A positive error will be decreased by the controller, while a negative error will be increased by the controller.

Applications of Analog Control Systems

The simplicity, reliability, and real-time operation of analog control systems, which eliminate the need for digital processing, make them suitable for a wide range of applications.

Industrial Automation:

Example: Utilizing analog controllers, such as proportional-integral (PI) or proportional-integral-derivative (PID) controllers, to control the temperature of industrial furnaces, the position of mechanical arms, and the speed of motors.

Benefits: For accurate industrial processes, analog control offers smooth, continuous control.

Consumer Electronics:

Example: Radio receivers with automatic gain control and audio amplifiers with volume control.

Benefits: High fidelity and fast response are features of analog control systems that are essential for high-quality audio and communication devices.

Automotive Systems:

Example: Controlling the anti-lock braking system's (ABS) performance and the internal combustion engine's fuel injection rate.

Benefits: Analog control improves vehicle performance and safety by ensuring a rapid and reliable response to changing conditions.

Basic Theory of Analog Control

Many engineering applications rely on analog control systems because they offer accurate and continuous regulation of dynamic processes. Understanding and creating efficient analog control systems requires a solid understanding of stability analysis and feedback loops. With a focus on feedback loops and stability analysis, this section explores the basics theory of analog control.

Feedback Loops

The foundation of control systems are feedback loops, which allow the system to adapt its behavior to variations in the output.

Open-Loop vs. Closed-Loop Control:

Open-Loop Control: Applies a fixed input to the process and functions without feedback. Although this approach is straightforward, it cannot fix errors brought on by disruptions or changes in the system parameters.

Figure 2: Open-loop control

Closed-Loop Control (Feedback Control): allows the system to fix errors and preserve the desired output by adjusting the input based on feedback from the output.

Figure 3: Closed-loop control

Components of a Feedback Loop:

Reference Input (Setpoint): the desired value that the system is trying to achieve.

Sensor: Measures the system's actual output and turns it to an electrical signal.

Comparator: Generates an error signal by comparing the measured output to the setpoint (Error = Setpoint - Measured Output).

Controller: Creates a control signal that powers the actuator by processing the error signal.

Actuator: Reduces error and moves the output closer to the setpoint by modifying the process in response to the control signal.

Types of Feedback:

Negative Feedback: Decreases errors by opposing output changes, improving system accuracy and stability.

Positive Feedback: Amplifies output changes, which, if not properly controlled, may cause instability.

Stability Analysis

A key component of control systems is stability, which guarantees that the system reacts to inputs and disturbances in a predictable and controlled way. After a disturbance, an unstable system deviates from equilibrium, whereas a stable system returns to equilibrium.

Definition of Stability:

Stable System: After a disruption, it returns to its equilibrium state.

Unstable System: After a disturbance, it deviates even more from its equilibrium state.

Marginally Stable System: It oscillates around equilibrium rather than approaching or departing from it.

Stability Criteria:

Bounded Input, Bounded Output (BIBO) Stability: If every bounded input leads to a bounded output, the system is said to be BIBO stable.

Lyapunov Stability: If a slight disturbance causes only slight deviations from equilibrium, the system is said to be Lyapunov stable.

Methods of Stability Analysis:

Root Locus Method: Examines how the characteristic equation's roots change as system parameters change.

Nyquist Criterion: The Nyquist plot is used to evaluate the stability of a feedback system by analyzing its open-loop frequency response.

Bode Plot: Illustrates the system's frequency response while showing phase and gain margins.

Routh-Hurwitz Criterion: Provides a systematic method for determining a system's stability by evaluating the characteristic equation without calculating for the roots.

Practical Considerations

Controller Design:

Proportional-Integral-Derivative (PID) Control: The most popular feedback control technique improves stability and corrects errors by combining derivative, integral, and proportional actions.

Proportional Control (P): The control signal is adjusted in proportion to the error. Provides a rapid response, but can result in steady-state error.

Integral Control (I): Integrates the error over time to remove steady-state error. Increases precision but may result in a slower response.

Derivative Control (D): Uses its rate of change to predict future errors. Increases response speed and stability but can amplify noise.

System Performance:

Transient Response: The response of the system to a disturbance or shift in the setpoint prior to steady-state.

Steady-State Response: The system's behavior after settling from a disruption or setpoint change.

Figure 4: Transient vs. steady-state response

Performance Metrics: Important metrics for assessing the operation of control systems include rise time, settling time, overshoot, and steady-state error.

Figure 5: Performance metrics

Types of Analog Control Methods

For the regulation of dynamic systems, analog control methods are crucial because they provide efficiency, accuracy, and stability. These methods fall within the broad categories of linear and non-linear control strategies. This section explores both categories, going into the basic principles and uses of key methods in each.

Linear Control Techniques

The input and output of the system are assumed to have a linear relationship in linear control techniques. These techniques are popular because of their ease of use, efficacy, and easy to understand mathematical foundations.

Proportional-Integral (PI) Control:

Proportional control and integral control are combined in PI control to improve transient response and remove steady-state errors.

Proportional Control (P): Generates a proportionate output to the error signal. The control signal u(t) is given by:

$$ u(t) = K_p e(t) $$

where e(t) is the error signal and Kp is the proportional gain.

Integral Control (I): Eliminates steady-state errors by gradually integrating the error signal. The following provides the control signal u(t):

$$ u\left( t \right) = K_i \int e(t) \, dt $$

where the integral gain is denoted by Ki.

Combined PI Control: In a PI controller, the control signal u(t) is:

$$ u\left( t \right) = K_p e\left( t \right) + K_i \int e(t) \, dt $$

Applications: frequently employed in industrial process control, motor speed control, and temperature control systems where preserving a steady setpoint is essential.

Proportional-Integral-Derivative (PID) Control:

To increase system stability and reaction time and predict future errors, PID control adds a derivative term to PI control.

Derivative Control (D): The following provides the control signal u(t):

$$ u(t) = K_p \frac{d e(t)}{dt} $$

where the derivative gain is represented by Kd.

Combined PID Control: In a PID controller, the control signal u(t) is:

$$ u\left( t \right) = K_p e\left( t \right) + K_i \int e(t) \, dt + K_p \frac{d e(t)}{dt} $$

Applications: Extensively employed in applications like robotics, aviation, and manufacturing processes that call for precise control and fast response.

Pole Placement Control:

Pole placement is the process of designing a controller that positions the system's closed-loop poles at desired locations in the s-plane, guaranteeing specific dynamic characteristics like damping, responsiveness, and stability.

Methodology: Involves figuring out the state feedback gain matrix K so that the closed-loop system has the appropriate eigenvalues (poles).

Applications: Utilized in modern control systems where precise dynamic performance is crucial, such as those in robotics, automotive, and aerospace.

Non-linear Control Techniques

Systems with a non-linear input-output relationship are addressed by non-linear control techniques. The complexity and non-linearities inherent in many real-world systems require the use of these techniques.

Hysteresis Control:

Within a predefined hysteresis band, hysteresis control, sometimes referred to as bang-bang control, alternates the control action between two states in response to the system's deviation from the setpoint.

Operation: Depending on whether the error is above or below a predefined threshold, the control action is either activated or deactivated.

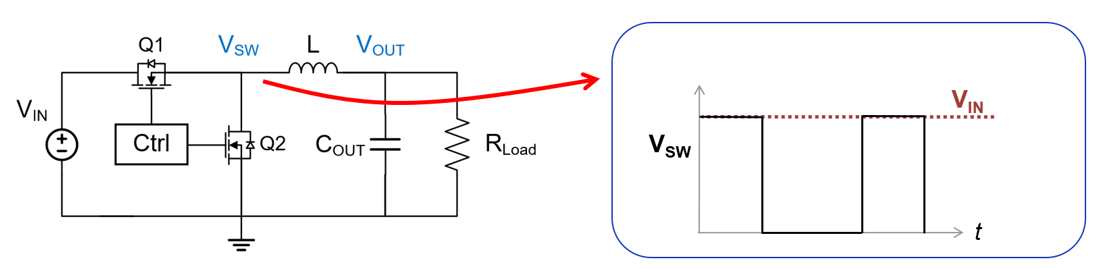
Applications: Frequently utilized in switching power supplies, power inverters, and thermostats where simplicity and fast switching are required.

Fuzzy Logic Control:

Fuzzy logic control offers a reliable method for modeling and controlling complex, non-linear systems by utilizing fuzzy set theory to manage uncertainties and approximate reasoning.

Components:

• Fuzzification: utilizes the membership functions to convert input values into fuzzy ones.
• Inference Engine: Generates fuzzy outputs by applying a set of fuzzy rules to the fuzzy input values.
• Defuzzification: Converts the control action's fuzzy output values back into crisp values.

Applications: extensively utilized in automotive systems (such as automatic transmissions and anti-lock brake systems), industrial process management where precise mathematical modeling is difficult, and consumer electronics (such as washing machines and cameras).

Advantages and Limitations of Analog Control Systems

The ability of analog control systems to regulate continuously and precisely has made them essential in many engineering applications. Designing and implementing efficient control strategies requires an understanding of the advantages and limitations of analog control systems. The key benefits and drawbacks of analog control systems are explored in this section.

Advantages

Real-Time Operation:

Immediate Response: Real-time operation of analog control systems eliminates the requirement for digital processing and analog-to-digital (A/D) or digital-to-analog (D/A) conversion, both of which have a finite processing delay. This feature enables an immediate response to system changes.

Continuous Signals: High-resolution control, which is essential for applications demanding precise and smooth regulation, is provided via the use of continuous signals.

Simplicity:

Straightforward Design: Compared to digital systems, analog control systems frequently have simpler designs and fewer components. This simplicity results in less expensive production and development.

Ease of Implementation: Fundamental analog control techniques, such proportional-integral-derivative (PID) control, are widely known and quite simple to apply using common analog components like operational amplifiers (op-amps), resistors, and capacitors.

Reliability:

Robust Performance: Analog control systems are renowned for their resilience and reliability, particularly in harsh environments where digital systems might be impacted by electromagnetic interference (EMI) and noise.

Minimal Software Dependency: Analog control systems are less susceptible to software bugs and vulnerabilities since they do not rely on complex software like digital control systems do.

Limitations

Noise Sensitivity:

Susceptibility to Interference: Analog signals are more prone to noise and interference, which can reduce system performance. External electromagnetic fields, thermal noise, and component imperfections can all cause errors.

Signal Degradation: Analog signals can deteriorate over long distances or through complicated circuitry, which might result in inaccurate control actions.

Component Variability:

Temperature and Aging Effects: The stability and accuracy of the control system might be impacted by temperature and age variations in analog components like resistors and capacitors.

Calibration Requirements: To sustain performance, analog systems frequently need to be calibrated on a regular basis, which increases maintenance work.

Limited Flexibility:

Fixed Functionality: In contrast to programmable digital systems, analog control systems are usually hardwired for specific operations, which limits their flexibility. Redesigning the circuit is frequently necessary to adjust the control algorithm or meet new specifications.

Scaling Challenges: It can be difficult to scale analog systems for larger-scale or more complicated applications because doing so may necessitate a significant redesign and additional complexity.

Precision and Accuracy Constraints:

Component Tolerances: The tolerances of the components that are employed limit the accuracy of analog control. It can be costly and challenging to find high-precision analog components.

Drift: Due to component aging and environmental changes, analog systems are susceptible to drift, or progressive variations in output over time, which can jeopardize accuracy and stability over the long run.

Power Consumption:

Higher Power Requirements: Compared to their digital counterparts, analog systems can consume more power, particularly in applications requiring high frequencies or speeds. In battery-powered or energy-efficient applications, this can be a major disadvantage.