Overview of Predictive Control in Power Electronics
Predictive control is a sophisticated control technique that has become quite popular in the power electronics industry because of its capacity to maximize performance in systems with complex dynamics and constraints. Predictive control predicts future system behavior by forecasting the evolution of the system's state using a mathematical model, in contrast to traditional control approaches that use feedback from past and present states to decide control actions. Predictive controllers can make well-informed decisions that maximize system performance across a predetermined prediction horizon because of this foresight.
Key Concepts in Predictive Control
Model Predictive Control (MPC): Model Predictive Control (MPC) is the most widely used predictive control technique in power electronics. It consists of:
- A model for the procedure
- A cost function is defined across the prediction horizon
- An optimization algorithm for minimizing the cost function
At each control step, MPC solves the optimization problem by minimizing the cost function, which usually contains terms for error tracking, control effort, and other system-specific requirements. The optimization is constrained by the system's physical limitations, such as voltage, current, and switching limits in power electronic devices.
An MPC controller performs the following tasks during operation:
- Forecasts how controlled variables will behave in potential switching states.
- It assesses the cost function for each prediction.
- Selects the switching state with the lowest cost function.
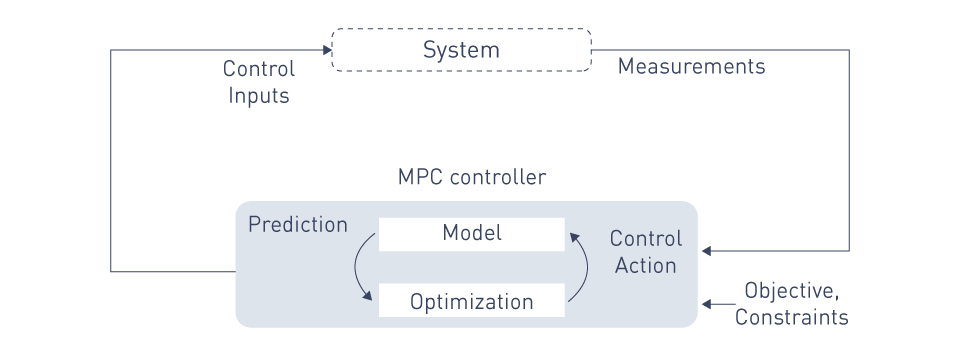
Figure 8: MPC concept
Prediction Horizon: The prediction horizon, or the period of time over which future system behavior is anticipated, is a critical component of MPC. One crucial design parameter that strikes a balance between control performance and computing complexity is the prediction horizon's length. Although it uses more computing power, a broader prediction horizon typically yields more accurate predictions and better control performance.
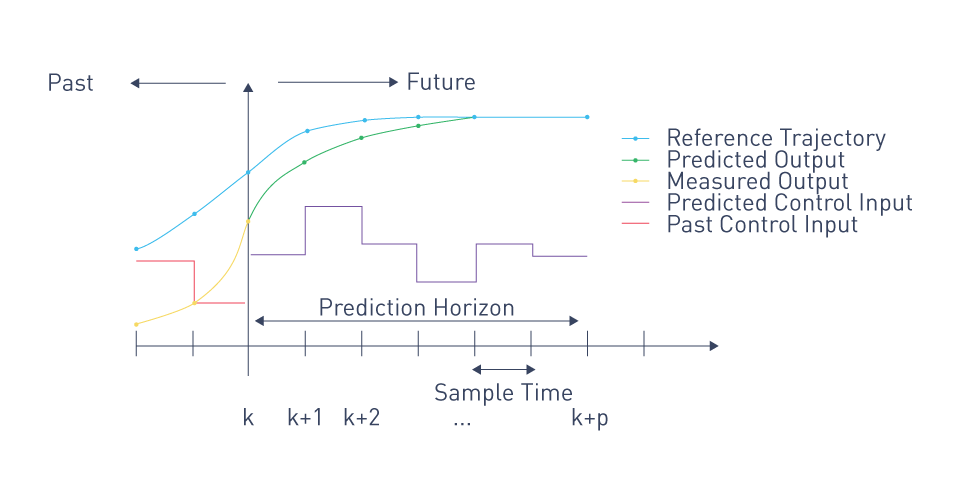
Figure 9: MPC scheme
Optimization Problem: MPC finds the best control actions at each sample instant by solving an optimization problem. The cost function and limitations are quadratic functions of the control inputs, and this problem is commonly expressed as a quadratic programming problem. The answer to this problem specifies the control measures that should be taken to minimize future deviations from the desired reference while remaining within system restrictions.
Receding Horizon Strategy: With MPC, just the first control action of the optimized sequence is implemented; the procedure is then repeated at the subsequent time step using updated state data. This is known as the receding horizon strategy. This approach guarantees that the control actions stay optimal as the system develops by enabling the controller to continuously adjust to changes in the system dynamics or external disturbances.
Applications of Predictive Control in Power Electronics
In power electronics, predictive control has several uses, especially in systems where traditional control methods are severely challenged by fast dynamics, nonlinearity, and constraints. Among the important uses are:
Inverter Control: Inverter control frequently utilizes predictive control, especially in applications where rapid response times and high-quality output waveforms are crucial. For instance, MPC can maximize efficiency and ensure grid code compliance in grid-tied inverters by optimizing the switching sequence to minimize harmonic distortion. MPC's predictive nature enables it to manage the switching limitations and nonlinearity that come with inverter operation.
Active Rectifiers: Predictive control also performs exceptionally well with active rectifiers. These devices, which are frequently used in power factor correction and regenerative braking systems, convert AC to DC with a regulated output. MPC can optimize the rectifier's switching sequence to reduce harmonic distortion, increase power factor, and minimize power losses while preserving stable performance under a range of input and load conditions.
DC/DC Converters: Predictive control can be used in DC/DC converters to keep the output voltage or current constant even when the input voltage or load varies. To reduce voltage ripple and enhance transient response, for example, MPC can forecast the future output voltage of a buck converter and modify the duty cycle accordingly.
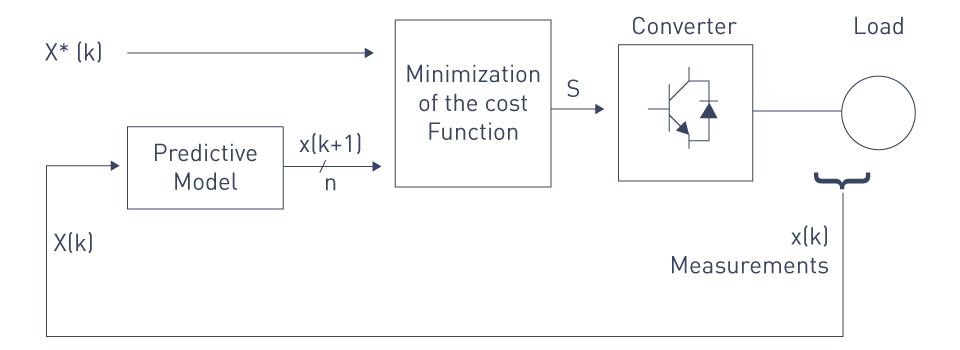
Figure 10: MPC scheme for power converters
Motor Drives: Predictive control is also becoming more popular in motor drives, where it provides benefits in dealing with the complex, nonlinear dynamics of electric motors. In real-time torque and speed control optimization, MPC can boost productivity and performance in robotics, industrial automation, and electric vehicle applications.
Advantages of Predictive Control in Power Electronics
Predictive control has numerous major advantages in power electronics, making it a preferred choice for many complex applications:
Handling of Constraints: The capacity of predictive control to explicitly address system restrictions, including switching constraints, heat limits, and voltage and current limits, is one of its most important advantages. The risk of damage to power electronic components is decreased by MPC, which guarantees that the control actions stay within safe operating limits by directly integrating these limitations into the optimization problem.
Improved Performance: Predictive control can considerably increase system performance by improving control actions in response to future predictions. Better reference signal tracking, faster response times, and less oscillations are made possible by this proactive strategy, which results in more steady and efficient operation.
Flexibility and Adaptability: MPC is naturally adaptable to a wide variety of power electronic systems and operating conditions. The cost function can be adjusted to prioritize various performance factors, such as power quality, efficiency, or harmonic distortion, and the predictive model can be updated to reflect for changes in system dynamics.
Robustness to Disturbances: In power electronics, where systems frequently operate in environments with substantial fluctuation and unpredictability, predictive control is especially useful because of its resilience to uncertainties and external perturbations, which is achieved by anticipating and compensating for disturbances.
Challenges in Implementing Predictive Control
Even with its advantages, predictive control implementation in power electronics has a number of challenges:
Computational Complexity: Significant computational resources are needed to solve the optimization problem in real-time at each sampling instance, especially in systems with high switching frequencies and fast dynamics. This challenge can be mitigated by streamlining the prediction model and cost function or by utilizing specialized hardware, like DSPs or FPGAs.
Model Accuracy: The efficiency of predictive control relies on the predictive model's accuracy. Performance degradation and inadequate control actions can result from inaccurate models. To make sure the model stays correct throughout time, methods for continuous model identification or adaptation can be utilized.
Parameter Tuning: MPC performance is susceptible to parameter tweaking, such as cost function weights and prediction horizon length. Achieving the ideal balance between computational load and performance requires careful tuning.
Essentials of Non-linear Control Theory
A branch of control theory that addresses systems whose behavior cannot be adequately described by linear equations is called non-linear control theory. The majority of systems in the real world are inherently non-linear.
Table 1. Linear vs. non-linear systems
| Property | Linear Systems | Non-Linear Systems |
| Superposition Principle | Holds true (output is the sum of individual responses) | Does not hold (output is not simply the sum of responses) |
| Mathematical Representation | Described by linear equations (e.g., y=mx+b) | Described by non-linear equations (e.g., y=x2 or y=sin(x)) |
| Proportionality | Direct proportionality between input and output | Output is not directly proportional to input |
| System Behavior | Predictable and consistent | May exhibit unpredictable or chaotic behavior |
| Additivity | Responses to combined inputs are additive | Responses to combined inputs are not necessarily additive |
| Stability | Typically stable (if the system is well-defined) | Can be unstable or sensitive to initial conditions |
| Response to Inputs | Output changes linearly with input variations | Output can change dramatically with small input variations |
| Time Invariance | Often time-invariant (properties do not change over time) | Can be time-varying (properties may change over time) |
| Analysis Techniques | Easier to analyze using tools like Laplace transforms and Fourier analysis | Requires complex methods like nonlinear differential equations, bifurcation analysis |
| Control and Optimization | Easier to control and optimize (e.g., linear controllers) | Harder to control and optimize due to complexity |
Non-linear systems exhibit complex behaviors, including multiple equilibria, limit cycles, bifurcations, and chaos, in contrast to linear systems, which operate on the principle of superposition, which states that the response to a combination of inputs is the sum of the responses to each input. Especially in power electronics, where many systems inherently display non-linear dynamics, these features make non-linear control challenging and offer loads of opportunities for innovative control strategies.
Understanding Non-linearity in Control Systems
Non-linear System Dynamics: If a system's output is not directly proportional to its input and its state-space representation includes non-linear functions of the input and state variables, it is considered to be non-linear. Saturation, dead zones, hysteresis, friction, and components like power electronic devices (such transistors and diodes) whose behavior cannot be linearized over the whole operating range are common causes of non-linearity in control systems.
Mathematical Representation: Usually, state-space models or non-linear differential equations are used to describe non-linear control systems. A general non-linear state-space model, for instance, can be represented as:
$$ \dot{x}(t) = f(t, x(t), u(t)) $$ $$ y(t) = g(t, x(t), u(t)) $$where f and g are non-linear functions of the states and inputs, x(t) is the state vector, u(t) is the control input, and y(t) is the output.
Equilibrium Points and Stability: Equilibrium points in non-linear systems (where the system remains at rest if not disturbed) are not always unique. Unlike linear systems, the stability of these points cannot be determined by simple eigenvalue analysis. Rather, non-linear control theory uses tools like Lyapunov functions, which construct a scalar function that decreases along system trajectories to provide a way to evaluate the stability of non-linear systems.
Key Concepts in Non-linear Control Theory
Lyapunov Stability: A powerful technique for analyzing the stability of non-linear systems is Lyapunov's direct method. A Lyapunov function, V(x), which is analogous to an energy function, is constructed as part of the procedure. A system is considered globally asymptotically stable if V(x) is positive definite and its derivative along the system trajectories, V˙ (x), is negative definite. This method, which ensures stability without requiring linearization, is frequently used to construct controllers for non-linear systems.
Feedback Linearization: Feedback linearization is a technique that uses feedback and a non-linear state transformation to convert a non-linear system into an equivalent linear system. The system's behavior can be controlled as though it were linear by implementing a control law that eliminates the non-linearities. This enables the use of linear control techniques. In power electronics, where systems such as converters and inverters can be linearized around a specific operating point, this technique is especially helpful.
Sliding Mode Control: Particularly useful in power electronic systems where robustness and rapid dynamic response are crucial sliding mode control is a robust non-linear control technique that makes the system "slide" along a predefined surface in the state space, called the sliding surface. Once the system reaches this surface, the dynamics that follow are made to be robust to specific kinds of disturbances and model uncertainties.
Backstepping: A recursive design technique called backstepping is used to stabilize non-linear systems in strict-feedback form. The controller's design is a step-by-step process that begins with the inner dynamics and works its way outward. A virtual control law is developed at each step, which eventually results in the actual control law. For managing non-linear systems with complex dynamics, such robotic or motor drive systems, backstepping is especially helpful.
Differential Flatness: When all system states and inputs can be represented as algebraic functions of a flat output and its derivatives, the system is said to be differentially flat. Trajectory planning and tracking in non-linear systems are made possible by flatness-based control, which takes advantage of this property to simplify the control problem. For tasks like trajectory generation in motor control applications, this concept is extremely essential to power electronics.
Non-linear Control in Power Electronics
The switching nature of power converters, the non-linear characteristics of components, and the interactions between various subsystems frequently cause power electronic systems to exhibit inherent non-linearities. To manage these complexities and reach the required performance levels, non-linear control techniques are crucial.
Non-linear Control of DC/DC Converters: The switching action of transistors and diodes causes DC/DC converters, such as buck, boost, and buck-boost converters, to naturally exhibit non-linear dynamics. Non-linear control techniques, such as sliding mode control, are employed to provide robustness against changes in load and input voltage as well as steady functioning under a variety of operating conditions.
Inverter Control: The output waveform of inverters, which convert DC power into AC power, must remain constant even when input conditions and loads change. High-quality sinusoidal outputs can be obtained while reducing harmonic distortion and enhancing dynamic response by using nonlinear control techniques like feedback linearization and nonlinear model predictive control (NMPC).
Motor Drives: Magnetic saturation, friction, and non-linear load torque are some of the factors why electric motors, especially those used in variable speed drives, exhibit non-linear characteristics. Backstepping and sliding mode control are two examples of non-linear control strategies used to increase the accuracy and resilience of motor control, which improves performance in applications like industrial automation and electric vehicles.
Challenges in Non-linear Control
Considering its advantages, non-linear control has a number of challenges:
Complexity: Compared to their linear counterparts, non-linear control systems are intrinsically more complicated, necessitating advanced mathematical tools and a thorough comprehension of system dynamics. Non-linear controller design, analysis, and implementation can become more challenging as a result of its complexity.
Computational Requirements: Non-linear control law implementation in real-time frequently requires a large amount of computational power, especially in systems with fast dynamics. In embedded systems with limited processing power, this could be a limiting factor.
Robustness to Uncertainties: Even while non-linear control is more capable of managing a wider variety of operating conditions than linear control, it is still highly challenging to guarantee robustness against model uncertainties and external disturbances. This is especially true in power electronics, where there is a lot of variation in the operating environment.
Table 2: Linear vs. non-linear controls
| Aspect | Linear Control | Non-Linear Control |
| Stability Analysis | Stability can be analyzed using linear methods such as Lyapunov’s or the Routh-Hurwitz criterion | Stability analysis is more complex and requires Lyapunov functions for non-linear systems, or numerical methods |
| Performance | Optimal for certain tasks when the system is well-modeled and operates within linear regions | Can handle more complex behaviors and provide better performance for systems with non-linearities |
| Design Complexity | Relatively simpler to design and implement | More challenging to design, requiring advanced control methods and deeper understanding of system dynamics |
| Response to Disturbances | Often assumes small disturbances or linear approximations to the system | Can handle large disturbances and more complex system behaviors |
| Adaptability | Linear controllers are generally less adaptive to changes in system parameters | Non-linear controllers can adapt to changes in system parameters more effectively |
| Linearization | Linearization is often used to approximate non-linear systems in practical design | Non-linear control does not require linearization, allowing it to directly address the inherent non-linearity |
| Computational Complexity | Computationally simpler and less resource-intensive | Requires higher computational power, especially for real-time control of complex systems |
Advantages of Predictive and Non-linear Control in Complex Systems
In managing complex systems, especially those with non-linearity, time-varying dynamics, and constraints, predictive and non-linear control techniques provide significant advantages. In several engineering fields, such as power electronics, robotics, aerospace, and process control, where traditional linear control techniques frequently fail, these control strategies are being used more and more. The following lists the primary advantages of predictive and non-linear control in complex systems.
Enhanced Performance and Accuracy
Predictive Control: Model Predictive Control (MPC), in particular, is excellent at maximizing system performance by predicting future states and minimizing a predetermined cost function through control decisions. Even in the face of disruptions and model inaccuracies MPC can improve output regulation and monitor reference signals more precisely by forecasting the system's future behavior over a specific horizon. Increased control precision and enhanced system performance are the outcomes of this ability of predicting and tackling future issues.
Non-linear Control: For example, non-linear controllers can better manage systems with saturation, hysteresis, and other non-linear phenomena than linear controllers, which may find it difficult to maintain accuracy in such conditions. Non-linear control techniques are specifically designed to handle systems whose behavior cannot be accurately modeled using linear approximations; these techniques take into account the intrinsic non-linearities of the system, resulting in more accurate control actions.
Robustness to System Uncertainties and External Disturbances
Predictive Control: Predictive control's robustness to external disruptions and system uncertainty is one of its major strengths. MPC can adjust to changes in the system dynamics or external conditions, ensuring steady and reliable operation because it continuously updates its predictions and control actions based on real-time data. In applications like power electronics, where input conditions, loads, and environmental factors can fluctuate rapidly, this resilience is especially useful.
Non-linear Control: Since non-linear control techniques are designed to operate under a wider range of conditions, they are inherently more resilient to changes in system parameters and external disturbances. Techniques such as sliding mode control and backstepping provide robustness against model inaccuracies and external disturbances, guaranteeing that the system maintains stability and performs well even when there are substantial uncertainties.
Ability to Handle Constraints
Predictive Control: The ability of predictive control, and MPC in particular, to explicitly handle system constraints is a significant advantage. Constraints on inputs, outputs, and states are crucial in many real-world applications and must be followed, for safe and effective functioning. By explicitly including these constraints into the optimization problem, MPC makes sure that the control actions don't go against operational, safety, or physical limits. In power electronics, where constraints on voltage, current, and switching operations are frequent, this feature is crucial.
Non-linear Control: Advanced non-linear techniques, including constrained optimization methods or adaptive backstepping, can be utilized to ensure that system constraints are maintained, even if handling constraints in non-linear control can be challenging. These techniques can offer more precise and practical control actions within the specified operational limits by incorporating non-linearities.
Flexibility and Adaptability
Predictive Control: Predictive control is extremely adaptable and can be adjusted to a variety of applications by altering the prediction model, cost function, and constraints. Because of its versatility, it can be used in a wide range of complex systems, including automotive and industrial operations, where operating conditions can change dynamically. Furthermore, MPC's receding horizon strategy allows for continuously modifying the control strategy in response to new information, which makes it very flexible to evolving conditions.
Non-linear Control: A broad spectrum of systems with complex, non-linear dynamics can benefit from the flexibility of non-linear control techniques. Non-linear systems can be made more tractable for control by linearizing or simplifying them using methods like feedback linearization and differential flatness. The ability to develop controllers that are precisely suited to the unique characteristics of a non-linear system offers an extended level of customization and adaptability that is not achievable with linear control techniques.
Improved Stability in Non-linear and Time-Varying Systems
Predictive Control: It is incredibly challenging to maintain stability in systems with time-varying or non-linear dynamics. By continuously adjusting control actions based on future predictions, predictive control provides a systematic approach to guarantee stability. MPC can stabilize systems that might otherwise be difficult to control using traditional approaches by considering future trajectories and constraints.
Non-linear Control: Techniques for non-linear control are especially designed to control the stability of non-linear systems. Lyapunov-based techniques, for instance, offer a strict framework for designing controllers that ensure system stability even when non-linearities are present. Another nonlinear approach, sliding mode control, offers robust stability by forcing the system to a stable sliding surface from which it cannot stray regardless of disturbances or uncertainties.
Optimized Energy Efficiency and Resource Utilization
Predictive Control: Predictive control can optimize energy consumption in applications where energy efficiency is crucial, such power electronics or process control, by foreseeing future demands and modifying control actions accordingly. For instance, by optimizing the switching sequences in a power converter according to anticipated load variations, MPC can reduce switching losses and increase overall efficiency.
Non-linear Control: Non-linear control techniques can also help optimize resource consumption by ensuring that the system operates at its most efficient level. Non-linear controllers, for instance, can optimize the motor's torque and speed in motor control applications, lowering energy consumption without sacrificing performance.
Case Studies: Implementation in Real-World Applications
Numerous real-world applications have efficiently implemented predictive and non-linear control approaches, especially in fields where system dynamics are complex, highly variable, and non-linear. These case studies illustrate the beneficial advantages and challenges of these advanced control techniques, showcasing how well they work to enhance system robustness, stability, and performance.
Case Study 1: Model Predictive Control in Grid-Tied Inverters
Background: In renewable energy systems like wind turbines and photovoltaic (PV) power plants, grid-tied inverters are crucial components that convert DC power from renewable sources into AC power that is compatible with the electrical grid. The inverter must maintain high power quality and efficiency while making sure that the output voltage and current are in sync with the grid. It is challenging to maintain stable and efficient operation of renewable energy sources due to their variability.
Implementation: Grid-tied inverters have adopted Model Predictive Control (MPC) because of their ability to manage several control objectives simultaneously. In this case, the MPC is utilized to optimize the inverter's switching sequence, minimizing harmonic distortion and guaranteeing that the output current follows a sinusoidal reference. The predictive model considers the fluctuation of the input power from renewable sources, the dynamics of the inverter, and the characteristics of the grid.
Results: MPC implementation in grid-tied inverters has resulted in considerable improvements in power quality, including lower Total Harmonic Distortion (THD) and better dynamic response to changes in input power. Additionally, by offering reliable control under a range of operating conditions, MPC has made it possible for renewable energy to be more effectively integrated into the grid. Predicting future conditions and modifying control actions accordingly has also increased the inverter's efficiency by lowering power losses and prolonging component life.
Challenges: Despite its advantages, implementing MPC in grid-tied inverters takes significant processing resources to solve the optimization problem in real-time. Dedicated digital signal processors (DSPs) and MPC algorithm optimization for faster execution have been used to overcome this challenge. For a deployment to be efficient, maintaining model accuracy and controlling computational complexity are still essential.
Case Study 2: Non-linear Control in Electric Vehicle Motor Drives
Background: Electric vehicles (EVs) use advanced motor drive systems for controlling the electric motors that power the vehicle. In order to maintain high efficiency and seamless operation, these motor drives must control the non-linear dynamics of the motor, such as changes in load, speed, and torque. Traditional linear control methods may struggle to deliver the appropriate performance over an EV's wide operating range.
Implementation: To address the challenges presented by the non-linear dynamics of electric motors, non-linear control strategies like backstepping and sliding mode control (SMC) have been implemented in EV motor drives. In this case, SMC utilizes a control law that drives the system to adhere to a preset sliding surface in order to regulate the motor's torque and speed. This method ensures steady operation even under changing load conditions by offering robust control against uncertainties and disturbances.
Results: The use of non-linear control in EV motor drives has improved torque control accuracy and dynamic response, resulting in better overall vehicle performance. SMC, in particular, has demonstrated efficacy in maintaining stability and robustness in the presence of nonlinearities such as magnetic saturation and friction. These enhancements result in longer battery life, better energy efficiency, and a more comfortable driving experience.
Challenges: Implementing non-linear control in EV motor drives presents design and tuning challenges as the control law must account for the motor's specific characteristics as well as the vehicle's operating conditions. Furthermore, real-time implementation requires large computational resources, necessitating efficient algorithms and hardware solutions. Ensuring robustness to model inaccuracies and external disruptions is also crucial for sustaining reliable performance.
Case Study 3: Predictive Control in Industrial Process Automation
Background: Maintaining optimal performance in the face of complex and time-varying dynamics in industrial process automation is essential for productivity and product quality. Traditional control methods are less effective in processes like temperature control systems, distillation columns, and chemical reactors because of their non-linear behavior and susceptibility to disturbances.
Implementation: To handle these complexities, Model Predictive Control (MPC) has been implemented in various kinds of industrial processes. Here, MPC is used to regulate a distillation column to preserve the output's intended concentration while using the least amount of energy possible. The non-linear dynamics of the process, such as the interplay between the column's several phases and the impact of disturbances on the output concentration, are taken into consideration by the prediction model.
Results: Energy efficiency and control accuracy have significantly increased as a result of the utilization of MPC in industrial process automation. MPC has made it possible to tighten control over product quality and lower energy consumption by optimizing control actions based on future predictions. This has improved process stability and reduced expenses. MPC's adaptability also makes it simple to adjust to changes in process configurations or operating conditions.
Challenges: The requirement for precise process dynamics modeling is the primary challenge in implementing MPC in industrial operations. Inaccurate models can result in instability or inadequate control performance. Furthermore, the MPC optimization problem's computational complexity necessitates the use of high-performance computing resources, which aren't usually accessible in industrial settings. Continuous model improvement and the utilization of efficient computational techniques are necessary to overcome these challenges.
Case Study 4: Non-linear Control in Robotics
Background: Robotics applications frequently entail controlling systems with complicated, nonlinear dynamics, such as robotic arms, mobile robots, and drones. These systems need to function precisely and reliably in dynamic settings where there are a lot of non-linearities introduced by interactions between multiple joints, actuators, and external forces.
Implementation: To overcome these challenges, non-linear control techniques have been used in robotics, such as adaptive control and feedback linearization. In this case, a robotic arm with several degrees of freedom is controlled by feedback linearization. The position and orientation of the arm can be precisely controlled by converting the non-linear system into an equivalent linear system, which makes the control problem easier to manage.
Results: Robotic systems' precision and responsiveness have significantly increased as a result of the use of non-linear control. Even when there are non-linear interactions between joints and actuators, feedback linearization has made it possible to track exact trajectories and regulate motion smoothly. These improvements have increased robots' capabilities to perform highly precise tasks including autonomous navigation, assembly, and surgery.
Challenges: The primary challenges to implementing non-linear control in robotics is the complexity of the control design, which needs to take into consideration the particular dynamics of the robot and the task at hand. Moreover, real-time control can have high computational demands, especially for robots with multiple degrees of freedom or those functioning in dynamic environments. Reliability additionally relies on robustness to external disturbances and model inaccuracies.










直接登录
创建新帐号