Introduction to Reference Circuits

An essential part of Analog-to-Digital Converters (ADCs) are reference circuits. They play a crucial role in preserving the correctness and integrity of the conversion process.

Role and Importance in ADCs

As the name implies, analog-to-digital converters transform continuous analog impulses into discrete digital representations. This conversion process's accuracy and dependability are essential in various applications, from precision measurement equipment to communication systems. Reference circuits help ADCs in a variety of ways, including:

Benchmark for Conversion: Reference circuits create a fixed standard for comparing analog inputs. For example, in a voltage-based ADC, the reference voltage sets the highest voltage to be measured. This standard helps decide the quantization levels and, ultimately, the accuracy of the ADC.

Stability Over Time and Conditions: For constant performance, the reference must be stable. A stable reference makes sure that the conversion stays accurate despite changes in temperature and supply voltage, especially in surroundings with these variations.

Improved Linearity and Reduced Errors: Non-linearity and inaccuracies in the ADC output are reduced by an accurate and reliable reference circuit. This is crucial in high-resolution applications where there is little room for error.

Dynamic Range Maximization: The ADC's dynamic range is determined by the reference circuit. The range of analog values that can be accurately converted to digital form can be increased by selecting a suitable reference voltage or current.

Types of Reference Circuits

Voltage References: These are utilized to establish a steady voltage level for comparison with the analog input voltage. Examples of common voltage references include bandgap references and Zener references, well-regarded for their ability to maintain stability even in the face of temperature fluctuations and changes in power supply.

Current References: Current references supply a dependable source of current. They play a crucial role in certain ADC architectures, like charge-redistribution ADCs, where a consistent current source is essential for precise charging or discharging of capacitors.

Reference Buffers: Frequently, rather than connecting the reference voltage or current source directly to the ADC, it is channeled through a buffer. Typically, this buffer takes the form of an operational amplifier, serving to ensure that the ADC input doesn't burden the reference source and thereby alter its value.

Programmable References: In some scenarios, having an adaptable reference proves advantageous. Programmable references empower users to select different reference levels to suit the specific requirements of an application, whether through digital adjustments or alternative methods.

Combined Reference Sources: In certain instances, especially in precision-critical applications, a fusion of reference sources may be deployed to attain an exceptionally high degree of stability or accuracy.

In conclusion, reference circuits are essential to the functionality and precision of ADCs. They guarantee that the digital output of an ADC correctly represents the analog input under a variety of circumstances by offering a consistent and accurate benchmark for conversion. For selecting or building a suitable reference for a certain ADC application, it is crucial to comprehend the many types of reference circuits and their features.

Voltage References

Particularly in Analog-to-Digital Converters (ADCs), voltage references are essential for establishing a stable voltage level that serves as a benchmark for other voltages to be measured or compared against. Voltage references come in many different varieties, each with its own unique qualities. Examining performance metrics including drift and noise, as well as Bandgap and Zener References, will be done in this part.

Bandgap References

Bandgap reference circuits are intended to generate a stable voltage under a range of environmental conditions. In order to achieve this, two voltages, one positive and one negative, with respect to temperature are generated and combined in a way that their respective effects are canceled out.

Operation: Bandgap references make use of the temperature-related behavior of a diode's voltage, combined with a Proportional to Absolute Temperature (PTAT) voltage, to create a stable reference voltage. The PTAT voltage increases with temperature, while the diode voltage decreases. By precisely combining these two effects, a voltage is generated that remains largely unaffected by temperature changes. Here's a detailed explanation of how the bandgap reference operates.

As mentioned earlier, the objective of the bandgap reference is to produce a consistent voltage that ideally doesn't fluctuate with changes in temperature or external influences. However, it's important to note that ambient temperature can impact the characteristics of various components within a circuit. For instance, the base-emitter voltage of a BJT transistor varies linearly with absolute temperature and has a temperature coefficient of approximately -2 mV/°C. These limitations of devices can influence the circuit's output.

If we lack access to superior devices, we'll need to find a way to offset the temperature-induced variations. For instance, if we can produce a voltage that's directly linked to absolute temperature and has a positive temperature coefficient of 2 mV/°C, we might be able to counteract the fluctuations caused by the base-emitter junction.

One approach to achieving the 2 mV/°C temperature coefficient is by recognizing that the thermal voltage (V_T) as described in the following equation, forms a linear relationship with absolute temperature:

$$V_T=\frac{kT}{q}$$

where k represents the Boltzmann constant, q stands for the charge carried by a single electron, and T represents temperature in Kelvin. The temperature coefficient of the thermal voltage is k/q (approximately +0.085 mV/°C), which is positive but falls short of the desired 2 mV/°C value. To address this issue, we can magnify the thermal voltage using a temperature-insensitive constant M, denoted as M∙k/q . This adjustment is made to ensure that M∙k/q equals roughly 2 mV/°C. This fundamental concept, at the core of a bandgap reference, is depicted in Figure 1 below. The "generator" block generates the thermal voltage. The output from this block is multiplied by an appropriate factor, represented as M, and then combined with the base-emitter voltage of a BJT. In an ideal scenario, the final output remains unaffected by temperature changes.

Figure 1: The example of bandgap reference circuit

Applications: Bandgap references find extensive use in ADCs, DACs, and power supply circuits, especially in scenarios where reliable operation is needed across fluctuating temperature conditions.

Zener References

When reverse-biased beyond the Zener voltage, the Zener diode has the ability to maintain a constant voltage across itself. This is how Zener references work.

Operation: The Zener voltage is the voltage at which a reverse-biased Zener diode begins to conduct. This value is useful as a voltage reference since it is essentially constant despite variations in the current flowing through the Zener diode.

Applications: Zener references are used in shunt regulators, ADCs, and any other situation where a straightforward, affordable voltage reference is needed. Their temperature stability, however, is frequently inferior to that of Bandgap references.

Performance Parameters

Voltage Drift: This refers to alterations in the reference circuit's output voltage due to shifts in ambient temperature. A minimal drift is preferred for maintaining accuracy across changing temperature environments. Generally, Bandgap references exhibit lower drift when compared to Zener 4references.

Noise: Noise within the reference voltage is crucial as it directly impacts the precision of ADC conversions. It's vital to minimize noise in applications that require high levels of accuracy. Methods like filtering and utilizing low-noise components are commonly used to reduce noise.

Load Regulation: The reference circuit's ability to sustain a consistent output voltage despite fluctuations in load current is known as load regulation. Effective load regulation ensures that the reference voltage remains steady under varying load conditions.

Long-Term Stability: This parameter reflects the reference's capacity to maintain accuracy over an extended period. Factors such as aging and stress can influence long-term stability.

Power Supply Rejection Ratio (PSRR): PSRR gauges how effectively the reference rejects variations in its power supply voltage. A high PSRR signifies that the output remains stable even when there are fluctuations in the power supply.

In conclusion, the careful selection of an appropriate voltage reference is a pivotal factor in ensuring the accuracy and dependability of ADCs and other analog circuits. Bandgap references are typically favored when temperature stability is a primary concern, while Zener references might be suitable for more straightforward and cost-conscious applications. An in-depth understanding and optimization of performance parameters such as drift, noise, and load regulation are essential elements in the design of robust and precise analog systems.

Current References

Current references hold equal importance to voltage references in various electronic applications. Instead of delivering a stable voltage, a current reference provides a consistent current, regardless of variations in voltage supply or load conditions. In this section, we will explore the fundamental principles and functions of current references and delve into their roles within Analog-to-Digital Converters (ADCs).

Basic Concepts and Operation

A circuit that produces a consistent output current is a current reference. Normal fluctuations in power supply voltages, temps, and load conditions have no effect on this steady current.

Operating Principle: Current references frequently make use of the characteristics of transistors that are active. In order to maintain a constant voltage across a resistor, one typical technique uses a bandgap voltage reference. According to Ohm's law, a constant voltage applied to a known resistance results in a constant current. A current mirror arrangement is another strategy that creates a stable output current by copying a reference current.

Widlar Current Source: The Widlar current source, a variation on the fundamental current mirror, offers a means of producing low reference currents with tolerable power dissipation and component sizes. This is accomplished by adding an emitter resistor to a current mirror, allowing the circuit to generate lower currents for a certain reference.

In the Widlar current source depicted in Figure 2, a resistor, denoted as R2, is placed in series with the emitter of the transistor Q2. Transistors Q1 and Q2 operate with dissimilar base-emitter voltages when R₂≠0. We will now proceed to compute the output current of the Widlar current source.

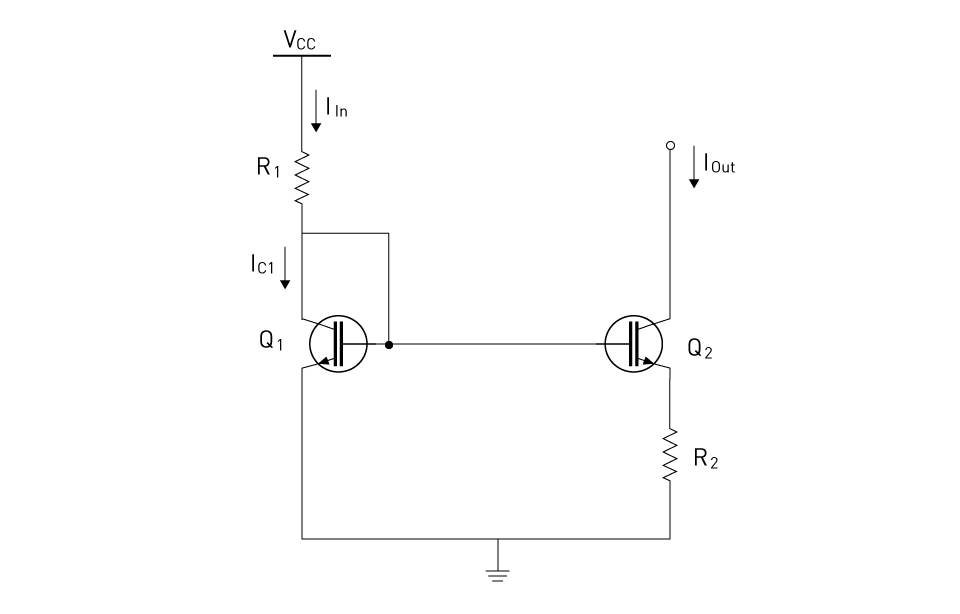
Figure 2: Widlar current source

If I_IN > 0, Q₁ functions in the forward-active region as a result of being diode connected. Assume that Q₂ also functions in the forward active region. Kirchhoff's Voltage Law around the base-emitter loop gives:

$$V_{BE1} - V_{BE2} - \frac{\beta_F + 1}{\beta_F} \cdot I_{OUT} \cdot R_2 = 0$$

where β_F is the forward current gain.

If we assume that V_BE1 = V_BE2 = V_BE(on), we would anticipate that I_OUT=0 . Nevertheless, it's worth noting that while I_OUT is typically small in practical applications, it is greater than zero under the usual bias conditions. This invalidates the standard assumption regarding V_BE(on) here. Conversely, the standard assumption often holds true when calculating I_IN because small variations in V_BE1 have little effect on I_IN if V_CC >> V_BE1 . However, when one base-emitter voltage is subtracted from another, even slight differences between them become significant. If the Early voltage V_A → ∞, the equation above can be rewritten as:

$$V_T \ln{\frac{I_{C1}}{I_{S1}}} - V_T \ln{\frac{I_{OUT}}{I_{S2}}} - \frac{\beta_F + 1}{\beta_F} \cdot I_{OUT} \cdot R_2 = 0$$

where V_T = kT/q is the thermal voltage and I_S1 and I_S2 are the transistor saturation currents.

If β_F → ∞:

$$V_T \ln{\frac{I_{IN}}{I_{S1}}} - V_T \ln{\frac{I_{OUT}}{I_{S2}}} - I_{OUT} \cdot R_2 = 0$$

For identical transistors, I_S1 and I_S2 are equal, and the last equation becomes:

$$V_T \ln{\frac{I_{IN}}{I_{OUT}}} = I_{OUT} \cdot R_2$$

This complex equation can be solved through a trial-and-error method to find the value of I_OUT if R₂ and I_IN are known, as is often the case in typical analysis problems. Since the logarithmic function tends to compress changes in its input, the focus can be primarily on the linear term within the last equation, making it easier to achieve convergence during the trial-and-error process. In design problems, however, the desired I_IN and I_OUT are usually known, so the required value of R₂ can be calculated.

Applications in ADCs

Biasing Circuits: In the realm of ADCs, current references are frequently applied to bias circuit components. Maintaining a stable bias current is vital for upholding the linearity and precision of the ADC across varying conditions.

Current-Steering DACs: In some ADC topologies, such as successive approximation ADCs, a Digital-to-Analog Converter (DAC) is incorporated into the operation. In current-steering DACs, precise currents are produced and shifted between various channels to create an analog output.

Charge Redistribution: Precise currents are required in certain ADC architectures, such as the pipeline ADC, this is to charge or discharge capacitors to particular values. To achieve great resolution and precision, this is essential.

Reference Generation for Comparators: The generation of references for comparators is a common practice in ADCs to measure the size of an input signal in relation to a reference. Through the use of a resistor, a stable current reference can be transformed into a stable voltage reference, which is then used by the comparators.

Reference Buffers

In reference circuits, reference buffers are a crucial component, particularly when the reference source needs to be shielded from changes in the load or when it is unable to give enough current to the load. In this section, we'll go over the function and usage of reference buffers as well as the crucial design factors that guarantee their effectiveness in ADCs and other electronic systems.

Purpose and Operation

Purpose: Reference buffers serve the essential function of separating a reference voltage or current source from the load. This separation is of paramount importance because reference sources, such as bandgap references, often possess limited current sourcing capabilities and may be susceptible to variations in the load. Buffers play a critical role in ensuring that the reference source retains its precision and stability by supplying the required driving strength to the load without imposing a burden on the reference source.

Operation: The operation of a reference buffer involves amplifying the current or voltage originating from a reference source, typically with a gain of one. This means that the output voltage matches the input voltage but has the capability to deliver a greater current. Reference buffers can be realized using operational amplifiers (op-amps) configured as voltage followers for voltage references or through transistors in a current buffer setup for current references.

Design Considerations

Input and Output Impedance: The reference buffer's input impedance should be high to guarantee that the reference source is not overloaded, while the output impedance should be low to give the load a powerful driving capacity.

Bandwidth: The buffer's bandwidth needs to be large enough to allow it to react to changes in load current demand without causing too many phase shifts or delays. In ADC applications where timing and speed are essential, this is extremely crucial.

Power Supply Rejection Ratio (PSRR): The buffer's ability to reject changes in its power supply voltage is measured by a metric called the power supply rejection ratio, or PSRR. To prevent power supply noise from coupling into the reference, a high PSRR is preferred.

Temperature Stability: To prevent the introduction of errors into the reference, it's important for the buffer to exhibit minimal drift across varying temperatures. This is typically accomplished through the thoughtful selection of components and strategic layout techniques.

Settling Time: In applications involving analog-to-digital converters (ADCs), the reference buffer needs to reach its stable state within a specified timeframe to adhere to sampling requirements. Reducing settling time is crucial for optimizing the performance of the ADC.

Noise: Minimizing the level of noise introduced by the buffer is essential, as it directly impacts the precision of the reference. Employing low-noise operational amplifiers (op-amps) and implementing meticulous printed circuit board (PCB) layouts can be beneficial in mitigating noise-related issues.

Reference Accuracy and Stability

The accuracy and stability of reference circuits are crucial to the overall performance of analog-to-digital converters (ADCs) and other precision electronics. In this part, the potential influences on reference circuit correctness are examined and discussed.

Factors Affecting Accuracy

Temperature Drift: Reference circuits frequently exhibit output variations in response to temperature changes. This temperature-induced instability can lead to significant inaccuracies, especially in applications that encompass a broad temperature spectrum.

Load Regulation: Alterations in the load current can impact the reference circuit's output voltage. Maintaining effective load regulation is vital for preserving accuracy when encountering fluctuating load conditions.

Supply Voltage Variations: Oscillations in the supply voltage can trigger adjustments in the output of the reference circuit. The power supply rejection ratio (PSRR) represents a critical metric for assessing how proficiently the reference circuit can counteract variations in the supply voltage.

Noise: Reference circuits inherently generate a certain level of noise. This noise can originate internally due to thermal effects or may be introduced from external sources. Such noise contributes to inaccuracies in the reference voltage or current output.

Long-term Aging: Over time, the components within the reference circuit may experience wear or deterioration. This aging phenomenon has the potential to result in drift in the reference output.

Initial Accuracy: The inherent precision of the reference circuit, as defined by the manufacturer, encompasses errors arising from manufacturing tolerances.

Techniques for Improving Stability

Temperature Compensation: Techniques such as the utilization of components with complementary temperature coefficients can be implemented to counteract the impacts of temperature-induced drift.

Feedback Control: The employment of feedback control mechanisms can be instrumental in sustaining a consistent output voltage or current, even in the face of load or supply voltage fluctuations.

Filtering and Decoupling: Filters and decoupling capacitors can be used to cut down on noise. High-frequency noise can be effectively filtered out using low-pass filters.

Using Precision Components: Precision capacitors, resistors, and other parts with low-temperature coefficients can improve the reference circuit's long-term accuracy and stability.

Calibration: Regular calibration of the reference circuit can assist in addressing accuracy-affecting issues like long-term drift. Techniques for software-based calibration may be included in this.

Buffering: By isolating the reference source from variations in load, a buffer (as explained in the preceding section), can aid with load regulation.

Using Bandgap or Zener References with High PSRR: By selecting reference sources with a high power supply rejection ratio, supply voltage swings are reduced to the least possible extent.

In conclusion, the performance of ADCs and other precision systems depends critically on the accuracy and stability of reference circuits. Reference circuits can deliver the dependable and constant performance necessary in high-precision applications by comprehending the aspects affecting accuracy and utilizing approaches to improve stability.