Range

The range of input voltages that an Analog-to-Digital Converter (ADC) may correctly read or process is known as the converter's "valid conversion range." Full-scale and +full-scale are the terms used to describe the lowest and highest positions in this spectrum, respectively.

When the -full-scale point is set to 0 Volts, the range becomes unipolar. However, the range is categorized as bipolar, when the -full-scale value reflects the +full-scale value as a negative voltage.

The ADC cannot deliver reliable conversion data if the input voltage is higher than this range. ADCs often respond to such an overrange condition by creating a code that aligns with the range endpoint that is closest to the input voltage that has been exceeded.

Resolution

Definition

The smallest difference in the analog input signal that an Analog-to-Digital Converter (ADC) can detect is referred to as resolution in this context. In essence, it refers to how many distinct levels the ADC can represent. An ADC with a resolution of N bits may represent 2^N distinct levels. Resolution is frequently given in bits. For instance, a 16-bit ADC may represent 2^16 levels, or 65,536, but an 8-bit ADC can represent 2^8 levels, or 256 distinct levels.

The ratio of the full-scale input range (the difference between the maximum and minimum input voltage) to the quantity of discrete levels (2^N) may also be used to mathematically define the resolution. The least significant bit (LSB), or ratio, denotes the smallest change in the input signal that the ADC can pick up.

$$1LSB = \frac {V_{ref}-V_{a} ^{gnd}}{2^n}$$

where:

LSB – Least significant bit

n – number of bits output by the ADC

V_ref – reference voltage

V_a^gnd – analog ground voltage

An ADC with n bit digital output, gives digital value "2ⁿ" which includes 0 and 2ⁿ -1.

If 5V is the reference voltage, then the resolution would be:

$$1LSB = \frac {5V}{2^{10}}=\frac {5V}{1024}=4.88mV$$

This depicts that for a change of 4.88 mV analog input, the digital value will be changed by 1 LSB.

Impact on Performance

The quality of the digital representation of the analog signal depends heavily on the resolution of an ADC, which has a considerable influence on its performance.

Quantization Error: Finer quantization is possible at higher resolutions, which lowers quantization error. The disparity between an analog value's true value and its digital representation is known as a quantization error. Higher-resolution ADCs are required in applications where accuracy is crucial, such as medical instruments or high-fidelity music.

Dynamic Range: The dynamic range of the ADC—the ratio of the biggest to the smallest signals that can be precisely measured—is closely connected to the resolution. The ADC can detect smaller changes when there are strong signals present- thanks to the increased resolution's extension of the dynamic range.

Signal-to-Noise Ratio (SNR): Higher resolution boosts SNR because the noise level, which is brought on by quantization error, is reduced while the signal intensity range is maintained. It is important to keep in mind, though, that if the ADC is not built with low inherent noise, increasing resolution may not necessarily result in a greater SNR.

Data Rate and Processing Requirements: Additional bits per sample come from an increase in resolution, which raises the data rate and necessitates additional data storage. This calls for greater processing power, which is crucial to take into account in embedded systems and other contexts with limited resources.

Conversion Time and Power Consumption: When using designs like SAR ADCs, high-resolution ADCs may need more time to transform an analog signal to a digital one. Additionally, choosing a greater resolution could make the ADC circuitry more complicated, which could lead to a rise in power usage.

Sampling Rate

Definition

The sampling rate, also known as sampling frequency, is a crucial ADC parameter that determines how many samples are obtained from a continuous analog signal per second. It is measured in samples per second (sps) or Hertz (Hz). How frequently the analog input signal is measured and transformed into a digital value is determined by the sample rate. Measurements are taken more often when the sample rate is higher than when the sampling rate is lower.

Relation to Nyquist-Shannon Theorem

The Nyquist Theorem, often known as the Nyquist-Shannon Sampling Theorem, is a fundamental idea that defines a standard for appropriately sampling a continuous signal without losing information. This theorem states that to reconstruct the original analog signal from its samples without aliasing, the sampling rate of a signal must be at least twice the bandwidth or highest frequency component of the baseband signal. The Nyquist Rate is the name given to this base rate.

Mathematically, this can be expressed as:

$$Sampling Rate ≥ 2 x Bandwidth$$

Consider a scenario where the sampling rate is lower than the Nyquist Rate. In that situation, a phenomenon known as aliasing may occur when the higher-frequency components of the signal can no longer be distinguished from the lower-frequency components. The digital version of the analog signal exhibits distortion and errors due to aliasing.

Impact on Performance

Resolution in Frequency Domain: A more thorough investigation of the signal's frequency components is possible due to higher sampling rates' improved frequency domain resolution. This is especially crucial in programs like digital signal processing and spectrum analysis.

Aliasing: As was already mentioned, sampling below the Nyquist Rate results in aliasing, which leads to distortion and information loss. This can be harmful in situations when maintaining the integrity of the signal is essential.

Data Rate and Storage: More data is produced per unit of time with a greater sampling rate. Due to the increased data flow and storage needs, systems with limited storage space may want to take this into account.

Processing Requirements: Particularly in real-time systems, a greater sampling rate could call for additional processing resources to manage the increased data stream.

Power Consumption: The ADC needs more power to function at a greater sampling rate. When it comes to battery-powered gadgets, where power consumption needs to be kept to a minimum, this might be a crucial factor.

Accuracy

Definition

An important ADC characteristic called accuracy measures how closely the digital output of the ADC matches the actual analog input value. In terms of Least Significant Bits (LSBs), percentage of full scale, or absolute voltage levels, it represents the systematic inaccuracy or departure of the measured value from the real value. In applications requiring precise measurements, such instrumentation and sensor data gathering, high accuracy is essential.

Offset Error, Gain Error

Several error components, the most frequent of which are offset and gain errors, can affect the accuracy of ADCs.

Offset Error: The offset error measures the difference between the ADC's real and ideal output values under a zero input voltage. It is the same for all output codes and is typically brought on by things like component mismatches or temperature changes. In most cases, offset error is indicated in LSBs or millivolts.

Gain Error: Gain error, without taking into account offset error, is the difference between the actual transfer function of the ADC and the ideal transfer function at full scale (maximum input voltage). Gain error, which represents how sensitively the ADC reacts to input voltage variations, is frequently brought on by internal component tolerances. LSBs or a proportion of the full-scale output are often used to express it.

Impact on Performance

Measurement Precision: The accuracy of the measurements can be considerably impacted by offset and gain problems. In applications like medical equipment, test and measurement equipment, and high-precision sensors, even little errors can have serious repercussions.

Calibration and Compensation: By measuring the errors at well-known reference sites and utilizing these measurements to account for the faults in software or hardware, offset and gain errors may frequently be calibrated. The system may become more complicated and expensive as a result of the calibration procedure.

Dynamic Range: Particularly offset problems might reduce the ADC's effective dynamic range since they may make the device saturate at lower input voltages than it would otherwise.

System Performance: The performance of a system can be impacted by inaccurate ADC measurements in feedback loops and control systems. For instance, inaccurate ADC readings in a temperature control system might lead to improper temperature management.

Reference Voltage

To generate the digital output, the ADC needs a reference voltage to which the analog input is compared. The analog input to reference voltage ratio determines the digital output:

$$digital value = \frac {V_{a}^{in}}{V_{ref}^{high}-V_{ref}^{low}} \cdot (2^n -1)$$

where:

V_aⁱⁿ – analog input voltage

V_ref^high – reference high voltage

V_ref^low – reference low voltage

n – number of bits of ADC digital output

For example, for 10-bit ADC if V_aⁱⁿ =1V and V_ref^high - V_ref^low =5V, the digital output is equal to:

$$digital value = \frac {1V}{5V} \cdot 1023=204d=0CCh$$

Linearity (DNL and INL)

Linearity is an important metric for ADCs since it indicates how closely the actual transfer function of the ADC resembles an ideal linear function. In other words, it defines the ADC's output values' departure from a straight line, also known as the ideal transfer characteristic. Linearity is critical in applications that demand exact signal amplitude replication, such as audio processing, measurement, and communications. Differential Non-Linearity (DNL) and Integral Non-Linearity (INL) are the two basic measures for analysing an ADC's linearity.

Differential Non-Linearity (DNL)

The difference in step sizes between neighboring digital output codes is quantified by differential non-linearity. The difference between neighboring output codes in a perfect ADC should be one least significant bit, or 1 LSB. The departure from this desired 1 LSB step size is what is meant by DNL. It is determined mathematically by:

$$DNL= (Actual step size between codes - 1LSB)$$

DNL is usually expressed in LSBs. A DNL value of 0 indicates ideal performance. A DNL error less than or equal to -1 may result in missed codes, which implies that the ADC may never create certain output codes regardless of the input, resulting in information loss.

Integral Non-Linearity (INL)

Integral non-linearity quantifies how far the ADC's transfer function strays from a line-like shape, illustrating the cumulative impact of DNL faults. In many cases, it is standardized to LSBs and measures the largest difference between the real and ideal transfer functions. According to mathematics, INL is the total of DNL errors up to a certain code in relation to the ideal transfer function:

$$INL = (Actual output code - Ideal output code)$$

Impact on Performance

Signal Distortion: The output quality is crucial in applications like audio or picture processing, where poor linearity (high DNL and INL) in an ADC can result in signal distortion.

Measurement Error: Measurement applications, such as sensors, will experience mistakes due to poor linearity. Some of these faults can be calibrated out, but the system becomes more complex in doing so.

Dynamic Range and Precision: Particularly in systems with low signal-to-noise ratios, non-linearity can have an influence on the effective dynamic range and accuracy of the ADC.

System-Level Performance: Non-linearity can bring errors into closed-loop control systems, which could result in instability or poor performance.

Noise Integral Non-Linearity (INL)

The random changes that are placed on the desired signal during the analog-to-digital conversion are referred to as noise in the context of ADCs. For digital representations of analog signals to be reliable and accurate, noise must be understood and managed.

Sources of Noise

Thermal Noise: Thermal noise, often referred to as Johnson-Nyquist noise, is produced by the erratically moving electrons within a conductor and is influenced by temperature, resistance, and bandwidth. It is a basically inevitable part of all electrical gadgets.

Quantization Noise: The ADC's limited resolution is the cause of this noise source. As an ADC can only represent a finite number of discrete levels, the real signal is approximated to the nearest level, which results in quantization errors.

Clock Jitter: Noise can come from fluctuations in the sample instances, which can be brought on by inaccurate and unstable timing of the ADC's clock.

Power Supply Noise: Power supply fluctuations and disturbances might link into the ADC and appear as noise in the converted signal.

Device Noise: The total noise performance can be influenced by manufacturing variances and intrinsic noise found in semiconductor devices (such transistors).

External Interference: The ADC input might couple with neighboring switching signals or other electromagnetic fields, adding more noise.

Signal-to-Noise Ratio (SNR), Noise Floor

Signal-to-Noise Ratio (SNR): SNR gauges how strong the intended signal is in comparison to the noise in the background. It is defined as the ratio of the power of the signal to the power of the noise and is often represented in decibels (dB). A signal that has a greater SNR is clearer and less noisy.

$$SNR (dB) = 10 \cdot log10 (Signal Power / Noise Power)$$

Noise Floor: The total amount of undesirable signals and noise in a measuring system is called the noise floor. It is the threshold below which transmissions are inaudible. In other words, it is impossible to measure signals that are weaker than the noise floor power. For sensing and measuring applications where the signals of interest may be very faint, the noise floor is a crucial metric.

To maximize the quality of the digitized signal, particularly in high-precision and high-sensitivity applications, it is crucial to comprehend and minimize noise in ADCs. ADC performance may be improved by the use of strategies including filtering, adequate shielding, and high-quality parts and power supply. To spread the quantization noise across a wider frequency range and hence boost the SNR, system designers frequently employ oversampling methods.

Dynamic Range

Dynamic range, which defines the range of amplitudes that the ADC can properly convert from analog inputs to a digital representation, is a crucial characteristic for ADCs. The ADC's capacity to record both low-level and high-level signals without distortion or saturation is measured by dynamic range. It is a crucial factor to take into account in applications like audio processing, imaging in the body, and radar systems where the input signal may display significant amplitude changes.

Definition

The ratio of the greatest (maximum) signal amplitude an ADC can handle to the least (minimum) signal amplitude it can consistently resolve is known as dynamic range. It is expressed in decibels (dB).

$$Dynamic Range (dB) = 20 \cdot log10 (Largest Signal Amplitude / Smallest Signal Amplitude)$$

Relationship with Signal-to-Noise Ratio (SNR) and Resolution

$$Maximum Dynamic Range (dB) ≈ 6.02 \cdot Number of Bits$$

This approximation results from the fact that the dynamic range is increased by about 6.02 dB for each extra bit of resolution.

Impact on Performance

Handling Wide Amplitude Variations: The ADC can correctly handle signals with a broad variety of amplitudes because of a larger dynamic range. This is crucial in situations like audio processing, where the input might range from quiet whispers to loud bangs.

Noise Performance: Better noise performance is often associated with a greater dynamic range, which enables more accurate measurements and increased signal fidelity, especially for tiny signal amplitudes.

Distortion and Clipping: Strong signals can surpass the maximum input range of the ADC if the dynamic range is insufficient, leading to clipping and distortion. On the other hand, noise can obfuscate weak signals that fall below the ADC's noise floor.

Considerations

Although a larger dynamic range is typically advantageous, it can sometimes have drawbacks, such as higher cost and power consumption. Therefore, it's crucial to pick an ADC with a dynamic range that matches the needs of the program.

Power Consumption

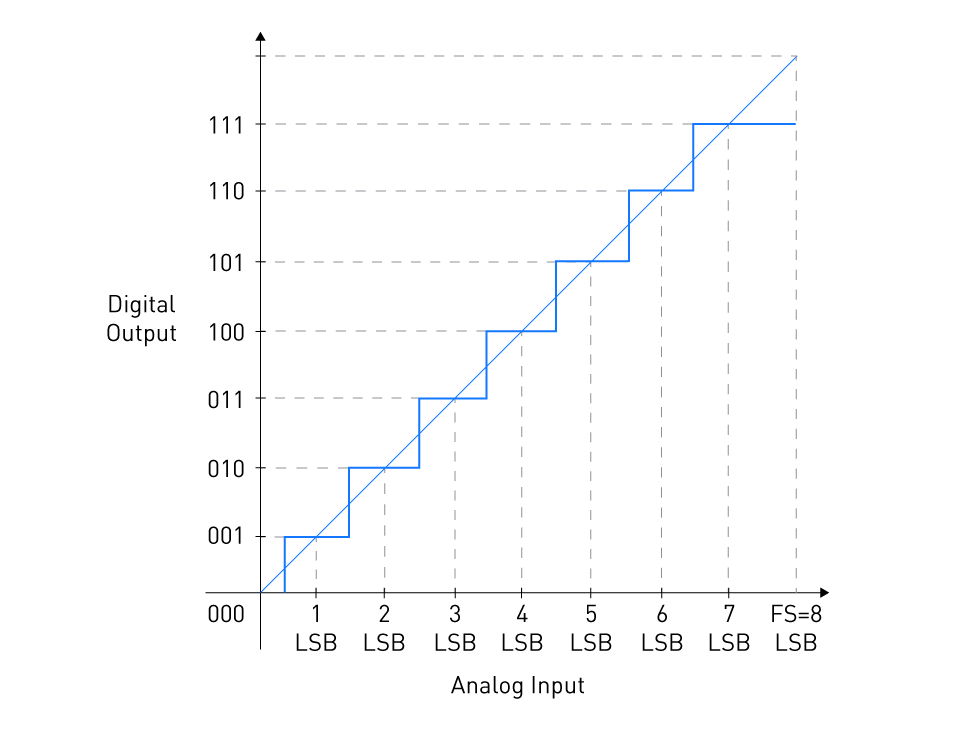
When developing and choosing ADCs, power consumption is a crucial factor, particularly in battery-operated and portable devices where power economy is crucial. It's essential to comprehend the aspects that affect an ADC's power consumption in order to maximize performance and battery life.

Static and Dynamic Power

Static power and dynamic power are the two basic types of power usage in ADCs.

Static Power:

The ADC uses static power when it is not actively processing signals or is idle. Leakage currents in the ADC's transistors are the main cause of this power. The operating frequency has little of an impact on the virtually constant static power usage. Modern low-power ADC designs strive to reduce static power, particularly in components destined for applications where the ADC may be idle for protracted periods of time, like sensor nodes.

Dynamic Power:

The power used by the ADC when it is actively operating, that is, when converting analog signals to digital values, is known as dynamic power. The operating frequency and the capacitive load that the ADC is driving determine the dynamic power. The following formula may be used to approximately estimate the dynamic power consumption:

$$P_{dynamic} = C \cdot V^2 \cdot f$$

where P_dynamic is the dynamic power, C is the capacitance being switched, V is the voltage, and f is the frequency of operation.

Low-Power Design Considerations

Resolution and Frequency Scaling:

Power consumption may be decreased by lowering the ADC's operation frequency or resolution. The resolution and bandwidth needs of the application must be matched with this, though.

Power Modes:

Power consumption may be optimized by utilizing several power modes, such as sleep, idle, and active modes. The ADC may be configured to utilize the least amount of power while not in use during sleep or standby mode. When necessary, it may then be immediately triggered.

Supply Voltage Scaling:

Both static and dynamic power consumption are decreased when the ADC is operated at a lower supply voltage. The performance impact must be taken into account, too, as a lower supply voltage may result in a decrease in the ADC's speed and noise performance.

Technology Choice:

Power consumption can be significantly impacted by the semiconductor technology chosen. For instance, CMOS-fabricated ADCs are often more energy-efficient than those made using older techniques like bipolar junction transistors (BJTs).

Architecture Selection:

ADC architectural selection is also crucial. For instance, sequential approximation register (SAR) ADCs are frequently utilized in low-power applications because they are typically more power-efficient than flash ADCs.

Input Impedance

Analog to digital converters (ADCs) must take input impedance into account while developing and using them. It plays a key role in how the ADC communicates with the hardware that is attached to its input. Input impedance and its significance in ADC applications is discussed in this section.

Definition:

Input impedance, often known as Z_in, is the ratio of voltage to current at the ADC's input. It expresses how much the ADC opposes or obstructs the passage of current into its input. It is provided mathematically by the relation:

$$Z_{in} = V{in} / I_{in}$$

where Z_in is the input impedance, V_in is the voltage at the input, and I_in is the current flowing into the input.

Input impedance might be resistive or reactive. The resistive component is often represented by resistance, whereas the reactive component might be represented by capacitance or inductance. Most of the time, especially at low frequencies, the capacitive aspect takes precedence, allowing the input impedance to be largely capacitive.

Importance:

Matching: When linking a source to an ADC, the source's impedance and the ADC's input impedance must be taken into account. To maximise power transmission and minimise signal reflection, proper impedance matching is required. In high-frequency applications, for example, impedance matching is critical to minimise distortion and signal integrity loss.

Loading Effects: A low input impedance ADC may use a substantial amount of current from the source. If the source has a high output impedance, a voltage drop (loading effect) might occur, resulting in a lower voltage being delivered to the ADC than intended. This tendency might cause errors in the converting procedure.

Bandwidth Considerations: At the ADC's input, the input impedance and parasitic capacitances can combine to generate a low-pass filter. This filter can limit the ADC's bandwidth and consequently the range of frequencies it can correctly convert. Understanding the input impedance enables adequate design considerations for bandwidth needs.

Noise Immunity: A high input impedance might make the ADC more vulnerable to noise since it acts like an antenna, taking up undesired signals. To reduce noise pickup in high-impedance applications, careful planning and design practices must be used.

Effective Number of Bits (ENOB)

The Effective Number of Bits (ENOB) notion is a critical parameter in evaluating the performance of an analog-to-digital converter (ADC). It gives a more accurate representation of an ADC's resolution by accounting for non-idealities like noise and distortion.

Definition

The number of bits in an ideal ADC with the same resolution as the ADC under test is denoted by ENOB. It measures the real resolution of the ADC when noise and distortion levels are taken into account. Typically, the ENOB is smaller than the ADC's nominal resolution (the number of bits in its digital output code).

The ENOB may be estimated using the Signal-to-Noise and Distortion Ratio (SINAD), which is measured in decibels and can be calculated as follows:

$$ENOB = (SINAD - 1.76) / 6.02$$

1.76 and 6.02 are constants derived from the conversion between dB and bits (20 * log10(2)).

Interpretation

When an ADC has an ENOB of, say, 10 bits, it operates the same as an ideal 10-bit ADC, although having a greater nominal resolution. The difference between the nominal resolution and the ENOB is caused by non-idealities in the ADC such as quantization noise, thermal noise, clock jitter, and non-linearities.

Importance

Understanding an ADC's ENOB is crucial for various reasons:

Performance Evaluation: ENOB offers a more accurate picture of the ADC's performance than simply looking at its purported resolution. Knowing the ENOB allows you to choose an ADC that satisfies the accuracy requirements of your application.

System Optimization: Engineers can detect limits in an ADC's performance by analysing the ENOB and making educated decisions about investing in higher-quality components or using signal processing techniques to increase accuracy.

Trade-offs: ENOB also aids in the comprehension of the trade-offs between resolution, bandwidth, and power usage. A lower-resolution ADC with a higher ENOB may outperform a higher-resolution ADC with a lower ENOB in some instances.

Data Integrity: It guarantees that data conversion accuracy is understood. This is especially important in high-precision applications, such as medical imaging, where data integrity is vital.

ADC Transfer Function

An ADC's transfer function is a graph that shows the input voltage in relation to the codes that the ADC produces.

See Figure 16 for the ideal transfer function of a 3-bit unipolar ADC.

Figure 16: Digital output vs. analog input (transfer function) of a 3-bit unipolar ADC

The input-output characteristic of the ADC should ideally be a uniform staircase. It should be noted that a single analog input value does not correlate to a single output code. Instead, each output code reflects a narrow input voltage range that is one LSB (least significant bit) wide. The initial code transition happens at 0.5 LSB in the preceding graphic, and each subsequent transition follows at 1 LSB. The final transition happens 1.5 LSB below the full-scale (FS) value.

The ADC displays a staircase response, which is intrinsically nonlinear, because a finite number of digital codes are utilised to represent a continuous range of analog values. The ADC transfer function can be usefully represented by the straight line that passes through the middle of the steps for analyzing certain non-ideal effects, such as offset error, gain error, and nonlinearity. The equation below may be used to represent this line:

$$Y_{linear}=\frac {V_{a}^{in}}{FS} \cdot 2^n$$

Where V_aⁱⁿ is the input voltage and n denotes the number of bits.

The staircase response would tend to become closer to the linear model as we keep on increasing the ADC resolution (or the number of output codes). As a result, the straight line may be thought of as the transfer function of a perfect ADC with infinite output codes. However, in practical use, we are aware that the ADC resolution is constrained and that the straight line is simply a linear representation of the response.

Understanding Datasheet and Specifications

Data sheets are essential tools in the engineering field because they contain thorough information on the specifications and performance of components such as ADCs (Analog-to-Digital Converters). A good comprehension of ADC data sheets and specifications is required for an engineer to make educated judgements during component selection and system design.

Key Components Of Datasheets

General Description: Typically, datasheets begin with a basic introduction of the ADC, highlighting its key uses and distinguishing features.

Absolute Maximum Ratings: This section specifies the maximum supply voltage and operating temperature that the ADC can sustain without causing irreversible harm.

Operating Ratings: This section describes the ADC's ideal working characteristics, such as standard supply voltage, operating temperature range, and average power usage. These values assure optimal performance and differ from Absolute Maximum Ratings, which reflect the component's extreme limitations without causing irreparable harm.

Electrical Characteristics: This is an important part that contains the operating specifications of the ADC, such as resolution, sampling rate, power consumption, input impedance, and others. It is usually displayed in the form of a table.

Functional Diagrams: Datasheets often include block diagrams illustrating the internal architecture of the ADC, which is useful for understanding its functioning and interface.

Pin Configurations and Functions: The pins of the ADC, their functions, and how to connect them are all described in this section.

Performance Graphs: These graphs show how the ADC works under various situations, including temperature, voltage, and frequency changes.

Application Information: This section describes how to utilise the ADC in various applications and offers sample circuits on occasion.

Package Information: It offers information on the physical dimensions and material qualities of the ADC's packaging.

Interpreting Specifications

Typical vs. Maximum Ratings: "Typical" values reflect regular performance, whereas "maximum" values show the boundaries beyond which the ADC may not work effectively.

Conditions: Many parameters are affected by environmental factors like temperature and power supply voltage. It is critical to understand the conditions under which the supplied specification is valid.

Parameter Correlations: A few variables are correlated. Increasing the sample rate, for instance, can result in higher power usage. When optimising a system, it is crucial to comprehend these relationships.

Practical Tips

Know Your Application Requirements: Be aware of the details of your application's needs before reading through data sheets. This will make it easier to concentrate on the pertinent specs.

Cross-Referencing: A datasheet may occasionally include contradictory or ambiguous information. Multiple sources, such as application notes, reference designs, and forums, should be consulted.

Ask for Help: If you have any inquiries or need the specs clarified, don't be afraid to get in touch with the manufacturer's support staff.