Introduction to ADCs in Test and Measurement

Overview and Importance

Analog-to-digital converters (ADCs) play a pivotal role in the realm of modern test and measurement equipment. Given that a majority of real-world signals exist in analog form, the conversion of these analog signals into digital format becomes an indispensable step for subsequent processing, analysis, and storage. Test and measurement equipment finds extensive use across various industries, serving purposes such as design validation, troubleshooting, and data collection. Whether the goal is to scrutinize the frequency spectrum, measure voltage levels, or capture high-speed signals, ADCs stand as the linchpin that empowers these instruments to function efficiently.

The significance of ADCs in the field of test and measurement can be attributed to several key factors:

Accuracy: The presence of high-accuracy ADCs ensures that the digital representation faithfully mirrors the analog signal. This precision is of utmost importance when aiming for exact and reliable measurements.

Speed: In instruments such as oscilloscopes and spectrum analyzers, the incorporation of high-speed ADCs becomes imperative. These components are essential for the swift and accurate capture of rapidly changing signals, which is often a fundamental requirement in test and measurement scenarios.

Resolution: The utilization of high-resolution ADCs allows for the detection of minuscule changes within the analog signal. This capability is indispensable in conducting sensitive measurements that demand the utmost precision and the ability to discern even the smallest variations.

General Requirements for ADCs in Test Equipment

Resolution: Test equipment often faces the need to discern subtle changes within a signal. Consequently, the resolution of the Analog-to-Digital Converter (ADC) emerges as a critical factor. Resolution dictates how finely a signal can be quantified, and it significantly impacts the level of detail that can be captured. To illustrate, a 16-bit ADC has the capacity to represent a signal using 65,536 discrete levels, providing much finer detail than a 12-bit ADC, which offers only 4,096 discrete levels.

Sampling Rate: The rate at which the ADC samples the analog signal is of paramount importance to ensure an accurate representation of the signal. This sampling rate must adhere to the Nyquist–Shannon sampling theorem, which sets the minimum requirement for accurate signal representation. In cases involving fast transient signals, it may become necessary to employ a sampling rate higher than the mandated minimum to faithfully capture signal dynamics.

Accuracy and Linearity: Accuracy entails how closely the ADC's output aligns with the true value of the input signal. Additionally, linearity errors, encompassing Differential Non-Linearity (DNL) and Integral Non-Linearity (INL) pertain to deviations in the ADC's transfer characteristic from a straight line. These non-linearities affect the uniformity of quantization levels, and they are particularly detrimental in high-precision applications where precision and consistency are paramount.

Noise Performance: A crucial consideration for ADCs in oscilloscopes is maintaining a sufficiently low noise floor to ensure that it does not obscure the signals of interest. An effective metric for assessing the ADC's overall performance is the Effective Number of Bits (ENOB), which takes into account both resolution and noise characteristics.

Dynamic Range: Dynamic range holds particular significance in applications like spectrum analysis. It quantifies the ratio between the largest and smallest signals that the ADC can accurately measure, providing a vital parameter for accurately capturing and analyzing signals with varying amplitudes.

Power Consumption: Depending on the specific application, the demand for low power consumption may be a critical requirement, especially in portable or battery-powered test equipment.

Interface and Compatibility: The chosen ADC must be compatible with the processing elements integrated into the oscilloscope system. It should offer suitable interfaces for efficient data transfer and seamless integration into the overall design.

ADCs in Oscilloscopes

Role in Signal Acquisition

For oscilloscopes, their primary role includes visually representing electrical signals over time, making them invaluable tools for testing, measuring, and analyzing various electrical signal characteristics. Within digital oscilloscopes, the pivotal role of Analog-to-Digital Converters (ADCs) becomes evident in the signal acquisition process. This process involves capturing the analog signal and converting it into digital format for subsequent display and analysis.

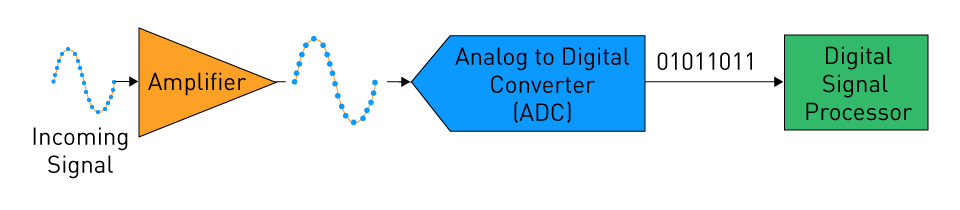
Figure 3: Signal flow through a digital oscilloscope

The journey begins with the analog signal, which can be either a voltage or current, undergoing conditioning through the input amplifier stage. Following this, the ADC steps in to sample the conditioned signal at regular intervals. For each sample, the ADC performs a conversion, transforming the analog amplitude at that specific moment into a corresponding digital value. These digital values are then stored in memory, allowing the oscilloscope to recreate the waveform accurately on its display for analysis and interpretation.

High-Speed ADC Requirements

Since high-frequency signals are frequently analyzed using digital oscilloscopes, the ADCs employed must be able to sample data at extremely fast rates. Some specifications for high-speed ADCs used in oscilloscopes include the following:

High Sampling Rate: High-speed ADCs employed in oscilloscopes must be capable of sampling signals at exceedingly high rates. This is essential to accurately capture and represent high-frequency signals. According to the Nyquist–Shannon sampling theorem, the ADC's sampling rate should be at least twice the frequency of the highest component within the signal of interest. However, in practical scenarios, significantly higher sampling rates are often favored to provide a more detailed and accurate representation of the signal's behavior.

Resolution: While achieving high-speed sampling is vital, it should not come at the expense of resolution. Striking a balance between resolution and speed is imperative. For many oscilloscope applications, the use of 8-bit or 12-bit ADCs is commonplace, as these provide an adequate compromise between detail and rapid data acquisition.

Low Latency: For real-time applications, minimizing latency is critical. Latency refers to the time delay between the input signal entering the ADC and the availability of the digital output. In high-speed oscilloscopes, especially those used for real-time analysis, minimizing this delay ensures that users can swiftly and accurately assess signal behavior.

Wide Bandwidth: The ADC should possess a wide bandwidth to encompass the entire frequency spectrum of the signal under investigation.

Example: High-Speed ADC in a Digital Oscilloscope

As an illustrative example, let's explore the application of a high-performance digital oscilloscope designed for the analysis of high-speed communication signals. In such a scenario, the oscilloscope is equipped with a high-speed Analog-to-Digital Converter (ADC) capable of achieving a remarkable sampling rate, often measured in giga samples per second (GSa/s). For instance, an ADC boasting a sampling rate of 5 GSa/s can accurately capture signals characterized by frequencies in the Gigahertz range.

One noteworthy ADC fitting this profile is the Texas Instruments ADC12DJ5200RF. This particular ADC is a 12-bit converter engineered to attain an impressive maximum sampling rate of 10.4 Gsps (Giga Samples Per Second). Its attributes make it exceptionally well-suited for applications demanding ultra-wide bandwidth and a high dynamic range. It finds extensive utility in high-performance digital oscilloscopes deployed for tasks such as RF signal analysis and the examination of high-speed communication systems, where the ability to capture and analyze signals with remarkable precision and fidelity is paramount.

ADCs in Digital Multimeters

Precision Measurement

Digital multimeters (DMMs) are flexible devices used to measure a range of electrical characteristics, including voltage, current, resistance, capacitance, and others. Analog-to-digital converters (ADCs) are essential to the functionality of DMMs since they enable precision measurement. Analog electrical quantities are converted into digital values that can be displayed and recorded by ADCs in DMMs. High precision, or the capacity to deliver measurements that are accurate and have a high resolution is a crucial feature of ADCs in DMMs.

Resolution and Accuracy Requirements

Resolution: In the context of an Analog-to-Digital Converter (ADC) within a Digital Multimeter (DMM), resolution refers to the smallest discernible change in an analog input signal that can result in a corresponding change in the digital output. DMMs often express resolution in digits, like 5½ or 6½ digits. A higher digit count signifies greater resolution. For accurate measurement in DMMs, it's crucial to have a high-resolution ADC to detect even the smallest variations in the quantity under examination.

Accuracy: Accuracy pertains to the proximity of a measured value to the actual or true value. In DMMs, accuracy is paramount, most importantly where precise measurements are essential for applications like calibration and testing. The ADC's integral and differential nonlinearity (INL and DNL) are key factors influencing the overall accuracy of the measurements.

Noise and Stability: Low noise levels and robust thermal stability are essential attributes of the ADC in a DMM. Noise can detrimentally affect measurement accuracy, and temperature fluctuations can introduce errors. Therefore, maintaining low noise and ensuring stable performance over varying temperatures are critical considerations.

Conversion Rate: While precision is of utmost importance, the conversion rate also holds significance, particularly for capturing transient events or rapidly changing signals. A sufficiently high conversion rate enables the DMM to effectively capture and represent dynamic or quickly changing quantities, ensuring the instrument's versatility across various measurement scenarios.

Example: High-Resolution ADC in a Precision Multimeter

Take the Agilent 34461A digital multimeter, a 612-digit Truevolt DMM, as an illustration, this multimeter is renowned for its remarkable accuracy and is utilized in high-precision measuring applications.

The high-resolution ADC present is one of the factors that contribute to its excellent precision. Such a high-precision multimeter may use an ADC with a resolution of 24 bits or greater. These ADCs have an incredibly fine resolution which enables the DMM to take measurements that are exceedingly accurate.

For instance, a 24-bit ADC may represent 2^24 or around 16.7 million discrete levels. It is essential for precision measurement applications like component testing, laboratory tests, and calibration services that it be able to detect even the smallest changes in the input signal.

ADCs in Spectrum Analyzers

Frequency Domain Analysis

Spectrum Analyzers: Spectrum analyzers are indispensable test instruments utilized by engineers and technicians to scrutinize the frequency components of various signals. These instruments excel in studying the spectral composition of electrical, acoustic, or optical waveforms. Unlike oscilloscopes which function in the time domain, spectrum analyzers operate exclusively in the frequency domain. They graphically represent the signal's amplitude on the Y-axis and its frequency on the X-axis. Spectrum analyzers are invaluable tools in numerous applications, including radio frequency (RF) design, audio analysis, and the development of communication systems.

In modern spectrum analyzers, Analog-to-Digital Converters (ADCs) assume a pivotal role in the signal analysis process. Their primary function is to convert the input analog signal into a digital format, enabling subsequent digital signal processing (DSP) algorithms to assess its frequency components. For spectrum analyzers to be effective, the ADC must possess the capability to accurately capture both the amplitude and phase of the input signal across a broad spectrum of frequencies. This accuracy is vital in ensuring the reliability and precision of spectral analysis in diverse applications.

ADC Performance Criteria

Critical criteria for ADCs used in spectrum analyzers are the following:

Dynamic Range: An imperative consideration for the Analog-to-Digital Converter (ADC) within spectrum analyzers is its dynamic range. This dynamic range is typically expressed in decibels (dB) and represents the ratio between the largest and smallest signals that the ADC can accurately measure. In the realm of spectrum analyzers, where signals often exhibit substantial variations in amplitude, dynamic range assumes paramount importance. A broader dynamic range equips the analyzer with the capability to precisely measure both robust and faint signals, even when they coexist.

Signal-to-Noise Ratio (SNR): The Signal-to-Noise Ratio serves as a crucial metric, measuring the relative power of the signal in comparison to the background noise power. A higher SNR signifies that the signal power significantly surpasses the noise level, a highly desirable condition. In spectrum analyzers, where the goal frequently involves the detection of low-level signals amid noise, a high SNR is imperative. The ADC should possess a commendable SNR to ensure that the noise originating from the ADC itself remains minimal, thereby preserving the accuracy of the measurements in the presence of external noise sources.

Sample Rate: The sample rate of the Analog-to-Digital Converter (ADC) serves as a pivotal factor governing the uppermost frequency that the spectrum analyzer can accurately measure. Adhering to the Nyquist theorem, the sample rate must be a minimum of twice the frequency of the highest component within the signal intended for analysis. A higher sample rate equips the spectrum analyzer to effectively capture signals with greater frequency content.

Resolution Bandwidth (RBW): Resolution bandwidth signifies the smallest frequency span that the spectrum analyzer can effectively resolve. A lower RBW allows for more intricate frequency analysis but necessitates a longer acquisition time. For the ADC within the spectrum analyzer, it is imperative to possess sufficient resolution to meet the desired RBW specifications. This ensures that the spectrum analyzer can finely dissect the frequency components of interest with precision.

Linearity: The ADC should exhibit excellent linearity characteristics, ensuring uniformity in the frequency response across the entire range of frequencies under analysis.