In-depth Analysis of Sinusoidal Waveforms

Understanding sinusoidal waveform characteristics is essential for studying and analyzing alternating current (AC) power theory. Sinusoidal waveforms, with their periodic oscillations, are essential for the transmission and distribution of electrical energy. This section goes into the complexities of sinusoidal waveforms, focusing on phase relationships, amplitude changes, and frequency implications, all of which are critical for understanding the behavior of alternating current power systems and electronics.

The sinusoidal wave's general equation is

$$y(t) = A \sin(\omega t + \phi)$$

In this case, the wave's value at any given time t is denoted by y(t), the amplitude by Α, the angular frequency by ω, and the phase by φ. The relationship between angular frequency and wave frequency is expressed as

$$\omega = 2\pi f$$

Here the frequency is denoted by f.

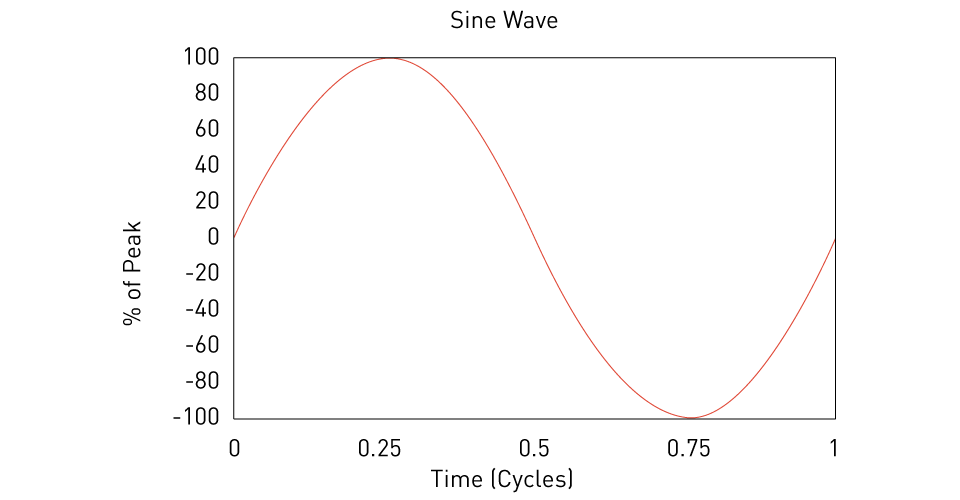
Figure 1: Sine wave

Phase Relationships

In sinusoidal waveforms, phase indicates the waveform's location with regard to a time-based reference point. In AC circuits, phase interactions are crucial, particularly when examining how the waveforms of voltage and current interact. The phase difference between two sinusoidal waveforms at the same frequency determines how they align with one another over time when they are compared. This phase difference—which is expressed in radians or degrees—can have a big impact on how well power is transferred in AC systems. For example, maximum power transfer occurs when voltage and current in a perfect resistive circuit are in phase.

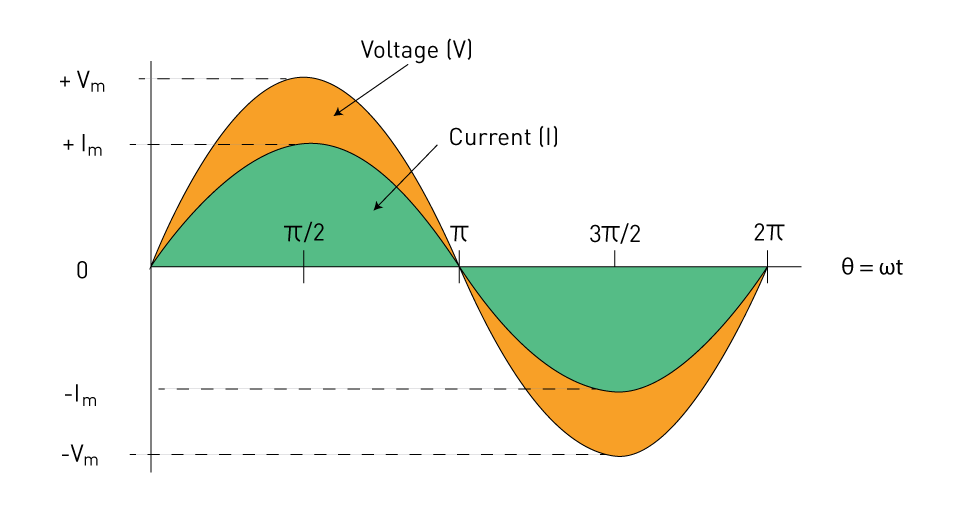
Figure 2: In-phase sinusoidal waveforms

On the other hand, voltage and current waveforms in circuits with inductive or capacitive elements may shift out of phase, producing reactive power that lowers the performance of the power system as a whole without generating any beneficial work.

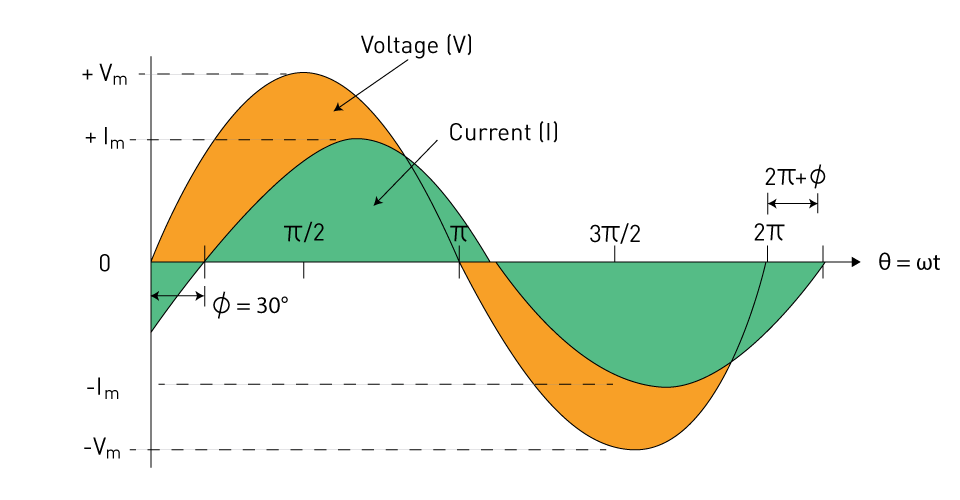
Figure 3: Sinusoidal waveforms with 30-degree phase difference

Amplitude Variations

A sinusoidal waveform's amplitude, or peak value, indicates the largest amount of variation or displacement from the waveform's equilibrium position. In electrical engineering, amplitude changes of sinusoidal waveforms are frequently monitored because they have a direct impact on power levels in AC circuits. The amplitude of the voltage and current waveforms indicates the amount of energy transmitted per cycle, and thus the power delivered to loads. Comprehending amplitude variations is also essential for building electrical systems that are reliable and resistant to harm by managing the highest anticipated loads within the system components' capacity.

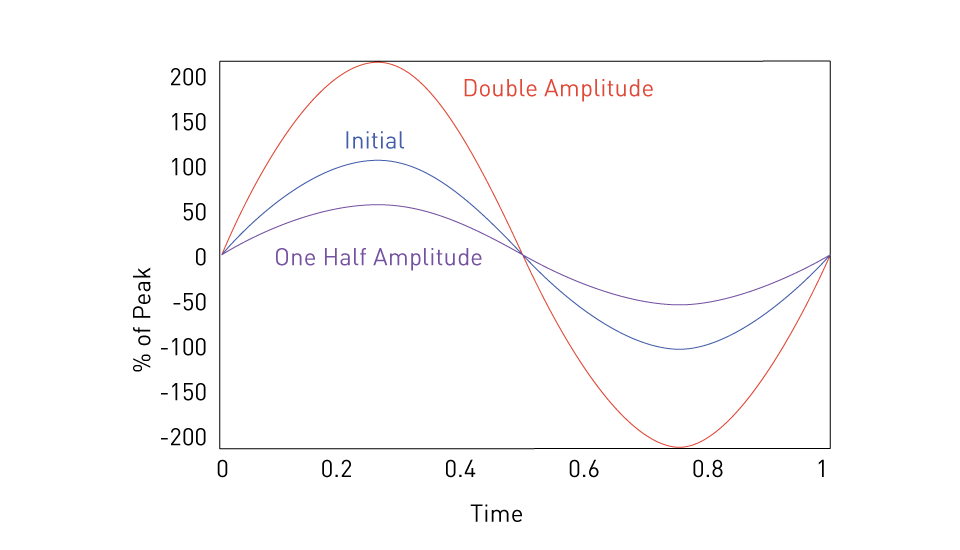
Figure 4: Amplitude variation

Frequency Implications

One of the characteristics that defines AC power systems is frequency, or the rate at which a sinusoidal waveform repeats per unit time. It has an impact on reactive parts like capacitors and inductors, which react differently at different frequencies, as well as the pace of energy transmission. Standard frequencies, such 50 Hz or 60 Hz, are set in electricity systems to guarantee grid stability and compatibility. Beyond simple compatibility, frequency implications affect how electrical and electronic devices are designed, how well power is transmitted, and how well frequency-sensitive devices function. For instance, the frequency-dependent variation in the impedance of inductive or capacitive elements influences the energy storage and release characteristics of these components over time. In order to maximize performance and efficiency, engineers must carefully examine these consequences while designing AC circuits and systems.

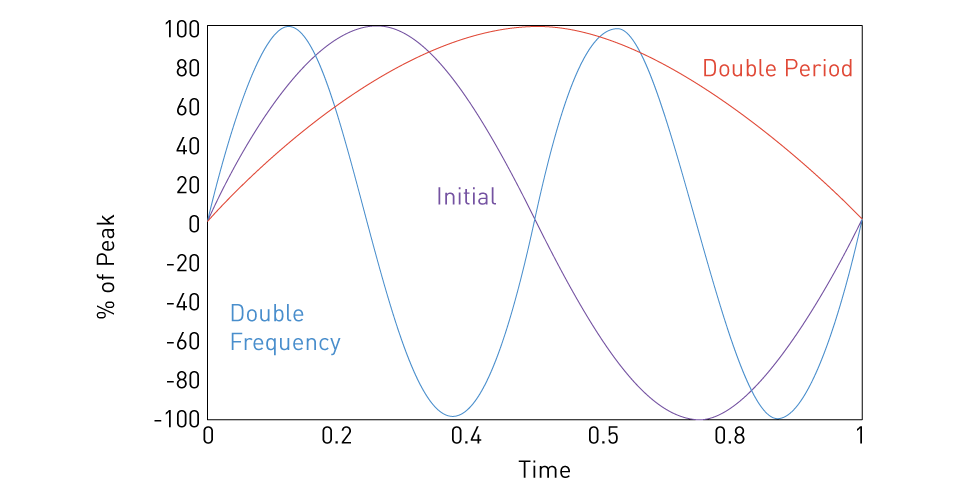
Figure 5: Frequency variation

Time Domain vs. Frequency Domain Analysis

The time domain and the frequency domain are two separate approaches that can be used to analyze electrical signals and systems. Each provides a different perspective on the properties and behavior of sinusoidal waveforms, which are fundamental to the theory and analysis of AC power. The contrast between time domain and frequency domain analyses is highlighted in this section, with a particular emphasis on the use of Fourier analysis to comprehend waveform composition.

Time Domain Analysis

Time domain analysis tracks signals as they change over time, giving a clear picture of the amplitude changes of a waveform at each instant. This method makes sense intuitively and is in line with how we see real-time electrical processes. Time domain analysis in the context of sinusoidal waveforms enables engineers to watch and quantify factors like amplitude, period, and phase straight from the waveform as it changes. Understanding the immediate behavior of AC circuits, including the long-term interactions between voltage and current inside different components, depends on this study.

Frequency Domain Analysis

In contrast, frequency domain analysis provides a unique perspective by focusing on the frequency components of a time-domain signal. This method is especially useful for evaluating complicated signals composed of many sinusoidal waves with varying frequencies, amplitudes, and phases. Engineers can detect and investigate specific sinusoidal components by converting a time-domain signal to the frequency domain, making it easier to analyze the signal's overall behavior and impact on an alternating current power system.

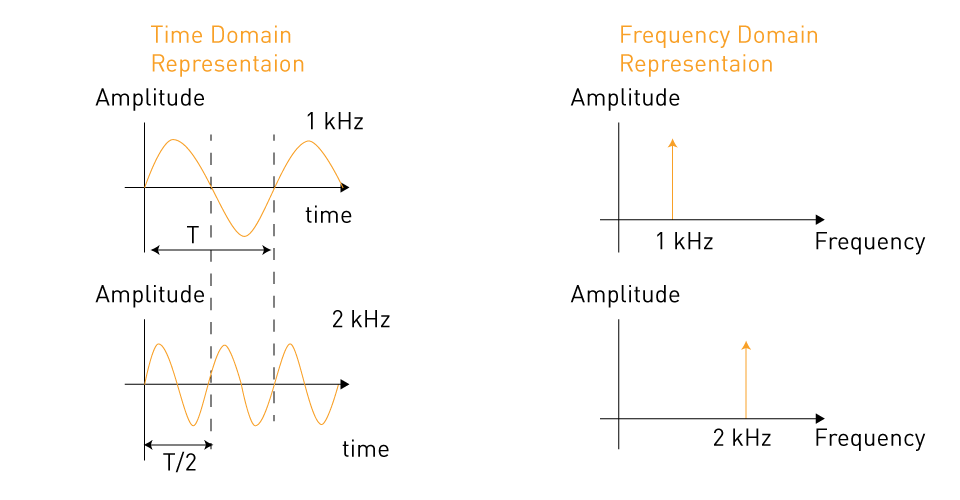
Figure 6: Time-domain and frequency-domain analysis of 1 kHz and 2 kHz AC signals

Fourier Analysis for Understanding Waveform Composition

Fourier analysis acts as a link between time and frequency domain investigations. This mathematical approach, named after Jean-Baptiste Joseph Fourier, converts any time-domain input into a sum of sine and cosine waves at different frequencies, each with its own amplitude and phase. This procedure, known as the Fourier Transform, shows a signal's frequency spectrum, giving a thorough representation of all the sinusoidal components that make up the original waveform.

The Fourier Transform mathematical equation for a continuous function is

$$F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} \, dt$$

where "t" is the time variable, "j" is the imaginary unit, and "ω" is the angular frequency (measured in radians per unit time). All of time is taken up by the integral.

Fourier analysis is a vital tool in engineering for the design, analysis, and optimization of electronic devices and AC power systems. It permits engineers to:

• Figure out a signal's frequency content, which is necessary for activities involving filtering, signal processing, and system design. Recognize how systems behave when exposed to various frequency signals, especially when analyzing resonance, bandwidth, and filtering properties.
• Analyze harmonic content and its implications on power systems, which includes power quality and harmonic filter design.

Real-world Implications

Sinusoidal waveform characteristics—phase, amplitude, and frequency—are critical to the operation of power systems and electronic equipment. These waveform qualities are more than just theoretical abstractions; they have significant real-world repercussions, influencing everything from electrical circuit design to the efficiency and reliability of power transmission and distribution networks. Understanding the impact of waveform characteristics on power systems and electronic devices is critical for electrical engineers who must optimize performance and ensure stability in a wide range of applications.

Effect on Power Systems

Sinusoidal waveform characteristics have a direct impact on the production, distribution, and transmission of electrical energy in power networks.

Phase Relationships: The power factor of an alternating current (AC) circuit is determined by the phase difference between the voltage and current waveforms. A power factor closer to 1 indicates that the circuit's power is being used effectively, while a lower power factor indicates the presence of reactive power, which does not perform useful work but still imposes a load on the system. Engineers strive to correct phase discrepancies to minimize losses and improve overall system efficiency.

Amplitude Variations: The amplitude of voltage and current waveforms influences the power delivered to a load. Overvoltage can cause equipment damage, whilst undervoltage can cause electrical devices to operate inefficiently or fail completely. Maintaining ideal amplitude levels is critical to the safe and efficient operation of power systems, necessitating the employment of voltage regulation equipment and preventative measures.

Frequency Implications: The frequency of the AC power system affects the functioning of synchronous machines as well as the network's resonance behavior. Deviations from the conventional operating frequency can cause inefficiencies, shorter equipment lifespans, and, in severe events, system instability. Frequency regulation is thus an essential component of system operations, especially in grids with a significant proportion of renewable energy sources, which might cause frequency variability.

Effect on Electronic Devices

Electronic equipment are designed to function within specified voltage and frequency ranges, therefore they are sensitive to changes in the characteristics of the AC power supply.

Sensitivity to Phase: Devices that rely on the phase relationship between voltage and current, such as certain types of motors and power electronics, might suffer performance problems or damage if the phase alignment is not within acceptable limits. Phase-sensitive applications necessitate careful design and frequently employ phase correction methods.

Amplitude Requirements: Generally, electronic gadgets have very specific voltage needs. While low voltage might cause problems or a lack of functionality, excessive voltage can cause overheating and component failure. Transformers and converters are examples of voltage regulation technologies that are essential to making sure that devices receive power at the proper amplitude.

Frequency Dependence: The operating frequency influences the behavior of devices that require accurate time signals, such as clocks and communication equipment. Variations in predicted frequency can disturb the operation of these equipment, emphasizing the significance of consistent and accurate frequency generation and control in power systems.