Designing a buck converter involves a systematic approach that can be broken down into distinct stages.
Specifications: Begin by clearly defining the specifications of the application. Determine the required input and output voltage, load characteristics, and any other relevant parameters.
Component Selection: Based on the specifications, select appropriate components such as the inductor, capacitor, and semiconductor switch. Consider factors like efficiency, cost, switching frequency, and the specific requirements of the application.
Calculations: Perform detailed calculations to determine key parameters such as inductance and capacitance values. These calculations ensure that the chosen components meet the specified performance criteria.
Finalizing the Design: Bring together the selected components and calculated values into a comprehensive design. Validate the design against the initial specifications and verify it using simulation tools and refine as necessary.
Choosing Components Based on Requirements
The selection of components is a critical aspect of buck converter design, driven by the specific needs of the application. When choosing components, it's essential to consider various requirements to ensure optimal performance.
Input Voltage: Select components capable of handling the anticipated input voltage range. Choose components such as the input capacitor and semiconductor switch that have voltage ratings (30%- 50%) above the maximum input voltage to ensure robustness.
Output Voltage: Tailor the design to achieve the desired output voltage. Ensure that the output capacitor and the feedback network are configured to maintain stable and accurate output voltage levels.
Current Rating: Choose components, especially the inductor and the semiconductor switch, with current ratings that exceed the maximum load current (20%-40%). This ensures that the components can handle the current demands without compromising efficiency or safety.
Output Power: Components should be selected based on the targeted output power. The semiconductor switch, inductor, and output capacitor should have power ratings that comfortably exceed the calculated output power to prevent overheating and component stress.
Switching Frequency: The switching frequency directly impacts the size of passive components. Higher frequencies may allow for smaller and lighter components, but they also increase switching losses. The choice of the switching frequency should strike a balance between size constraints and efficiency.
Output Voltage Ripple: Components, especially the output capacitor, should be selected to minimize output voltage ripple. A low ESR (Equivalent Series Resistance) capacitor can help reduce ripple and improve the overall performance of the buck converter.
Thermal Requirements: Components must be chosen to meet thermal requirements. Select a semiconductor switch with a thermal resistance suitable for the operating conditions and consider heatsinking or other thermal management techniques to ensure that the components operate within their specified temperature limits.
By carefully considering these requirements, engineers can choose components that not only meet the electrical and power specifications of the buck converter but also ensure reliability and longevity in the application. This comprehensive approach to component selection is crucial for designing a buck converter that performs optimally across a range of operating conditions.
Calculating Key Parameters
Consider factors such as load current, switching frequency, and acceptable ripple voltage. Precise calculation of key parameters is fundamental to ensuring the functionality and efficiency of the buck converter.
Inductance: Calculate the required inductance (L) to maintain a stable output voltage.
$$L= \frac {V_{IN} - V_{OUT} \times D}{f_s \times ∆I_L}$$where VIN is the input voltage, VOUT is the desired output voltage, D is the duty cycle of the switch, fs is the minimum switching frequency, and ΔIL is the desired peak-to-peak inductor current ripple. ∆IL is given as:
$$∆I_L = \frac {(V_{in} - V_{out}) D}{f_{sw} \times L}$$Where Vin is the input voltage, Vout is the output voltage, D is the duty cycle, fsw is the switching frequency and L is the value of the inductance.
Capacitance: Determine the capacitance necessary for smoothing the output voltage. This involves accounting for ripple voltage and load variations.
$$C= \frac {ΔI_L}{8 \times f_s \times ∆V_{OUT}}$$where ΔIL is the inductor ripple current, D is the duty cycle, f_s is the switching frequency, and ΔV_out is the acceptable output voltage ripple.
Switching Frequency: The switching frequency affects various aspects of the buck converter, and it can be calculated as:
$$f_s= \frac {V_{IN} \times (1-D) \times D}{L \times∆I_L}$$where VIN is input voltage and D is the duty cycle, L is the inductance value and ∆IL is the peak-to-peak ripple current.
Output voltage ripple: The output voltage ripple is influenced by the capacitance and the load, and it can be estimated using the above equations:
$$∆V_{OUT} = \frac {ΔI_L}{8 \times C \times f_s}$$Where IL is the inductor current, D is the duty cycle, fs is the switching frequency, and C is the value of the output capacitor.
These equations provide a solid foundation for designing a buck converter tailored to specific application requirements. Engineers can leverage these formulas to optimize the performance of the converter, ensuring stable output voltage, minimal ripple, and efficient power transfer.
Design Example
Design a buck converter topology for:
$$V_{in} = 100V, V_{out} = 12, \Delta V_{out} = 1\%, \Delta I_L = 100mA, f_{sw} = 10kHz, R = 10\Omega$$Solution:
1. Find Duty Cycle.
$$D=\frac {V_{out}}{V_{in}}$$ $$D=\frac {12}{100} = 0.12$$2. Find the value of output current.
$$I_{out}= \frac {V_{out}}{R} = \frac {12}{10} = 1.2A$$3. Find the value of Capacitor required.
$$C_{min}=\frac {ΔI_L}{8 \times f_{sw} \times ∆V_{out}}$$ $$C_{min} = \frac {0.1}{8 \times 10k \times 0.12} = 10.4uF$$We may take it as 15-20uF.
Find the value of inductor.
$$L=\frac {(V_{in}-V_{out})\times D)}{f_{sw} \times ∆I_L}$$ $$L=\frac {(100-12) \times 0.12}{10k \times 0.1A} = 8.8mH$$So to remain in CCM mode it is good to go with L≥8.8mH. We may take it as 10mH.
4. Find the rating of switches.
The switch (MOSFET) must be selected carefully when designing the buck converter. Its reverse voltages may be greater than the 1.5x the output voltage of the boost converter. In our example:
$$ V_{ds_{switch}} ≥ 300V$$Where Vds is the maximum drain to source voltages. The input current will be the current passing through the MOSFET. Theoretically:
$$P=I_{in} V_{in}=I_{out} V_{out}$$ $$I_{in}=1.2 \times \frac{12}{100} = 0.144A$$The current rating of the MOSFET switch will be 1.5x of the input current:
$$I_{switch} ≥ 0.2160A$$The frequency of MOSFET must be greater than the application need. Like for our application:
$$f_{sw} ≥ 10kHz$$Feeback Topology for Buck Converter
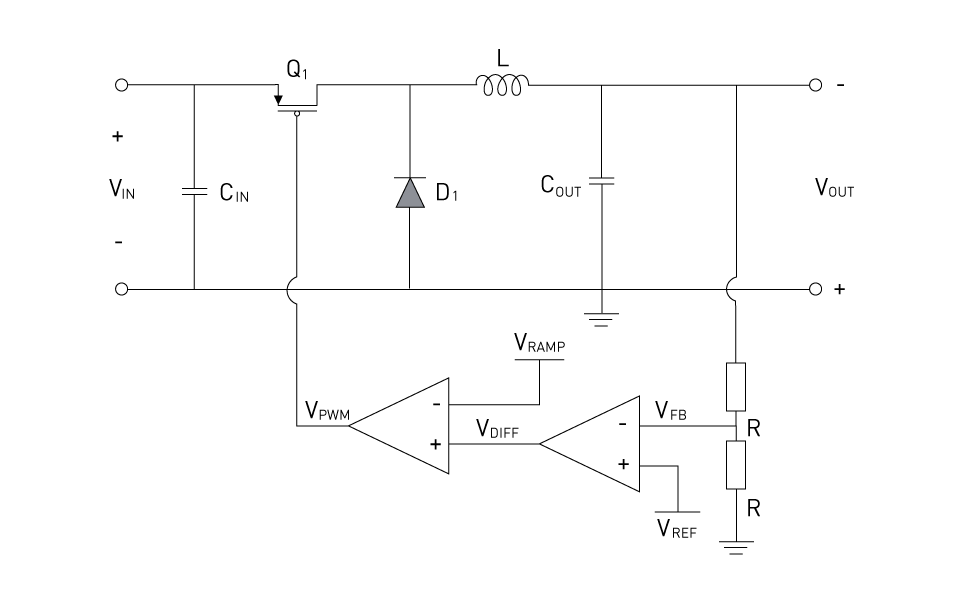
Figure 9: Feedback for Buck Converter
A feedback topology for buck converter is shown in the figure above. The voltage divider feedback is the most common and widely used accepted feedback technique. The output of this divider VFB is compared with the Vref reference voltage of the buck converter (set voltage). The error voltage Vdiff is compared with the Vramp (ramp voltage of a fixed frequency) to produce a PWM of the duty cycle proportional to the output voltage. The values of these feedback resistors are very much critical as feedback operation relies on them.
Vout can be set by knowing the reference voltage and the values of these feedback resistors.
$$V_{out}= V_{ref} \frac {R_{FBT}+R_{FBB}} {R_{FBB}}$$Initially the Vout is known (designed output voltage), we may find the values of feedback resistances from this equation.
$$R_{FBT}=R_{FBB} ( \frac {V_{out}}{V_{ref}} -1)$$RFBB may be chosen between 20-200 kΩ and RFBT can be calculated. It should be noted that higher values of these resistances can affect stability of the op-amp, while lower values will draw unnecessary amounts of current resulting in lower efficiency.

直接登录
创建新帐号